В литературе методов расчета одиночных вибраторов, конфигурация которых отличается от прямолинейной, известно относительно не много [61–65], тем более, не известны методики расчета ЛПВА с кусочно-линейными вибраторами, основанные на строгих методах.
Заменим в ЛПВА [1] (рис. 1.1), расположенной в свободном пространстве, прямолинейные вибраторы на кусочно-линейные (рис. 5.1). Ось y декартовой системы координат (ДСК) направим вдоль линии питания антенны, ось z, расположим так, чтобы вибраторы “лежали” в плоскости y0z.
Каждое
плечо m-ного симметричного кусочно-линейного вибратора
состоит из S сегментов одинакового радиуса 
с длинами hm,j.
Вектор, направленный из точки питания m-го
вибратора в начало j-го сегмента n-го
вибратора, обозначим через rsm,n,j, а вектор единичной длины, направленный вдоль сегмента номер j m-го вибратора, обозначим как axm,j. Расстояния от начала координат до точек питания вибраторов обозначим
через ym, а длины плеч вибраторов –
.
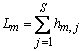Они изменяются в зависимости от номера m в геометрической прогрессии со знаменателем t, т. е.
Вибраторы питаются переменнофазно распределительной линией. Считаем, что вибраторы выполнены из металлических трубок с бесконечной проводимостью и диаметры трубок много меньше длин вибраторов и длины волны.
Для определения электродинамических характеристик такой ЛПВА необходимо определить распределения токов по вибраторам антенны, по которым можно найти КНД, КСВ в фидере антенны и ДН.
Очевидно, что для определения распределений токов по кусочно-линейным вибраторам ЛПВА возможно использовать уравнения (1.40) с изменениями в ядре, которые будут учитывать взаимное положение линейных наклонных отрезков вибраторов антенны. Поэтому рассмотрим методы расчетов распределения тока одиночного криволинейного вибратора и, выбрав наиболее выгодный, обобщим его на систему вибраторов ЛПВА. Из [21] известно, что определение распределения тока по изогнутому тонкому вибратору возможно с использованием интегральных уравнений Поклингтона, Галлена или Мея [61]. На основе этих уравнений разработаны методы расчета влияния изгиба вибратора на распределение тока [61–63]. Однако, при расчетах всеми этими методами возникает трудность – появление операции дифференцирования под знаком интеграла в ядре уравнения для токов. Но в работе [64] получено на основе уравнения Галлена относительно простое и достаточно точное и удобное при расчетах интегральное уравнение для тока кусочно-линейного вибратора, в котором устранена операция дифференцирования в ядре. Исходя из отмеченного, используем для определения распределения тока по кусочно-линейному вибратору методику работы [64].
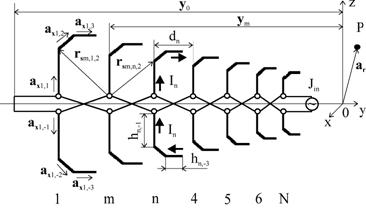
Рис. 5.1. ЛПВА с кусочно-линейными вибраторами
Решение задачи о нахождении распределений токов в вибраторах ЛПВА с кусочно-линейными вибраторами отличается от решения задачи для ЛПВА с прямолинейными вибраторами (1.28–1.40) учетом взаимного влияния линейных сегментов в ядре ИУ (1.40). Поэтому сначала решим задачу об определении распределения тока по одиночному кусочно-линейному вибратору, а затем полученное решение перенесем на случай ЛПВА.
Распределение тока по кусочно-линейному вибратору и поле, созданное этим током, должны удовлетворять уравнениям Максвелла [47], записанным для комплексных амплитуд векторов напряженностей электрического и магнитного полей (1.16), когда отсутствуют тепловые потери в среде.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.