Логопериодические вибраторные антенны: Учебное пособие, страница 18

.

Подставляя  в предыдущее выражение, объединяя интегралы, и умножая числитель и знаменатель правой части на  получаем интегральное уравнение Галлена

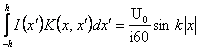,                         (1.27)

где ядро интегрального уравнения

.

1.4. Система интегральных уравнений Галлена для токов в вибраторах

До сих пор все выкладки делались для одиночного вибратора. ЛПВА представляет собой систему из N вибраторов и для анализа этой антенны будем пользоваться методикой, изложенной в [11]. Учтём, что в ЛПВА присутствуют вибраторы разной длины и для уменьшения зависимости характеристик антенны от частоты весьма желательно у каждого n-го вибратора обеспечить постоянное отношение  длины вибратора к его радиусу. На практике это возможно только в печатных антеннах и при необходимости мы будем это учитывать, вводя для каждого вибратора своё отношение . Для ЛПВА (рис. 1.1) получаем систему ИУ относительно неизвестных токов

,            (1.28)

где                       ,                                          (1.29)

При выводе ИУ Галлена для одиночного вибратора принято в (1.20), что ЭМ поле поверхностного тока с плотностью , текущего по боковой поверхности вибратора радиуса  параллельно его оси, при отсутствии азимутальной вариации тока эквивалентно ЭМ полю линейного тока, протекающего по оси цилиндра с плотностью . Таким образом, мы заменили плотность поверхностного тока, текущего по боковой поверхности вибратора, плотностью линейного тока, текущего по оси цилиндра. Однако, в этом случае в выражении для функции Грина –, при  , так как при этом . При совпадении точек интегрирования и наблюдения . Если строго следовать этому приближению, то при интегрировании (1.20) в точке  подынтегральное выражение обращается в бесконечность и эту особенность необходимо учитывать при расчётах. Кроме того, в этом случае пренебрегают зависимостью результатов расчётов от радиусов вибраторов.

Но для системы вибраторов расстояния  и  не могут обратиться в нуль при . Если  из-за разноса вибраторов по оси , то в этом случае можно положить радиус вибратора  равным нулю. С учётом этих соображений расстояния  и  выражаем следующим образом

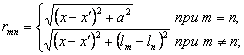
(1.30)