Логопериодические вибраторные антенны: Учебное пособие, страница 57

Векторы напряженностей электрического и магнитного  полей (комплексные амплитуды) могут быть выражены через векторный потенциал :

К каждому j-тому сегменту m-го вибратора привяжем локальную систему координат с осью , направленной вдоль оси сегмента. Считаем, что ток сегмента имеет одну компоненту, параллельную оси , касательная составляющая вектора напряженности электрического поля на поверхности сегмента равна нулю, а в точке соединения сегментов электрический ток непрерывен.

Запишем выражение для вектора  на поверхности каждого сегмента вибратора:

.              (5.1)

В дальнейшем изложении опустим точку над векторами. Выразим из (5.1) касательную к поверхности вибратора компоненту вектора напряженности электрического поля  и, приравняв ее к нулю (касательная составляющая вектора напряженности электрического поля на поверхности идеального металлического тела должна равняться нулю), в результате получим дифференциально–разностное уравнение для векторного потенциала:

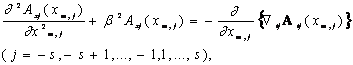,               (5.2)

где A_xj(x_m,j) и A_tj(x_m,j) – осевые и поперечные составляющие векторного потенциала A_j(x_m,j), , e₀, m₀ – электрическая и магнитная постоянные и , – векторный оператор набла.

Уравнение (5.2) – известное неоднородное дифференциально-разностное уравнение, решение которого имеет вид

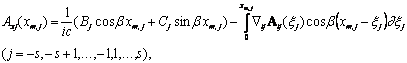,           (5.3)

где B_j, C_j – произвольные постоянные интегрирования, c – скорость света в вакууме. После дифференцирования A_xj(x_m,j) (5.3) по переменной x_m,j и принимая во внимание условие Лоренца, скалярный потенциал

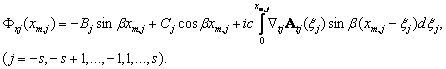   (5.4)

Постоянные интегрирования B_j, C_j, найдем из (5.4) и граничных условий:

A_j(h_j)=A_j+1(0), при j=1,2,...,s-1,                                   (5.5,a)

Ф_j(h_j)=Ф_j+1(0), при j=1,2,...,s-1,                                  (5.5,b)

A_j(h_j)=A_j-1(0), при j= -s,-s+1,...,-1,                              (5.5,c)

Ф_j(h_j)=Ф_j-1(0), при j= -s,-s+1,...,-1,                              (5.5,d)

A₁(0)=A_-1(0),                                                                (5.5,e)

Ф₁(0)=-Ф_-1(0)=U₀/2,                                                      (5.5,f)

где U₀ – напряжение на клеммах питающей линии ЛПВА в точке подключения вибратора.

В дальнейшем будем явно рассматривать только величины, определенные в области l £j£s, так как вибратор симметричен. Подстановка (5.3) и (5.4) в граничные условия (5.5a) и (5.5b) позволяет получить уравнения для постоянных интегрирования: