Физические основы микроэлектроники, конспект лекций, страница 7

Интегрирование дает

,

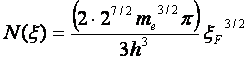откуда получим после преобразования

.

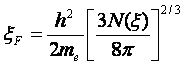Для указанного в задаче числа электронов имеем

.

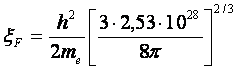После подстановки констант окончательно получим

 эВ.

2.4.1. КОНЦЕНТРАЦИЯ ЭЛЕКТРОНОВ И ДЫРОК В ПОЛУПРОВОДНИКЕ.

Пусть при некоторой установившейся температуре полупроводник находится в состоянии термодинамического равновесия, которое характеризуется равенством скоростей генерации и рекомбинации. В единичном объеме полупроводника находится определенное количество  свободных носителей заряда, которое называется концентрацией.

          Концентрацию электронов в зоне проводимости можно получить, проинтегрировав полную функцию по всем энергиям зоны проводимости:

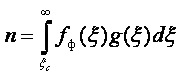,                                               (2.14)

где g(x) – функция плотности состояний электронов в зоне проводимости [5].

          В результате интегрирования получим:

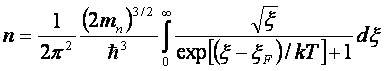.                 (2.15)

         Интервал в выражении (2.15) получил название интеграла Ферми порядка ½. Аналогичное выражение можно получить для концентрации дырок в валентной зоне:

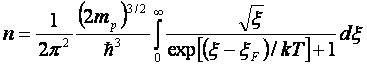.                    (2.16)

         Величины m_p и m_n в выражениях (2.15) и (2.16) – это, так называемые эффективные массы электрона и дырки, соответственно. Они определяются соотношением:

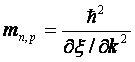.                                               (2.17)

Если полупроводник является невырожденным, то, с учетом того, что единицей в знаменателе подинтегральной функции в (2.15) и (2.16) можно пренебречь, получим приближенное выражения для концентраций носителей:

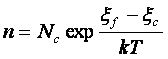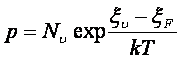; ;                       (2.18)

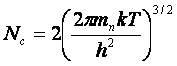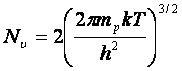;.               (2.19)

N_c, N_u - эффективные плотности состояний в зоне проводимости и в валентной зоне.

2.4.2. ПОЛОЖЕНИЕ УРОВНЯ ФЕРМИ И КОНЦЕНТРАЦИЯ НОСИТЕЛЕЙ ЗАРЯДА В СОБСТВЕННОМ ПОЛУПРОВОДНИКЕ.

В собственном полупроводнике положение уровня Ферми находится из условия равенства электронов в зоне проводимости  и дырок в валентной зоне

,                                                  (2.20)

индекс i  в (2.20) обозначает принадлежности к собственному проводнику. Приравнивая правые части для  n и p в (2.18) и решая относительно ξF, получим:

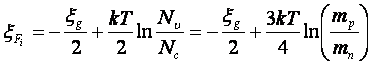,                            (2.21)

где ξg – ширина запрещенной зоны собственного полупроводника.           Подставив полученной выражение для ξ_Fi (2.21) и (2.18) получим выражение для концентрации носителей заряда в собственном полупроводнике:

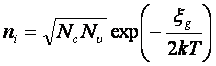.                               (2.22)

Часто выражение (2.22) удобно представлять в логарифмическом масштабе:

.                                         (2.23)