Физические основы микроэлектроники, конспект лекций, страница 10

Рис. 2.5. Зависимость концентрации носителей от температуры в примесном полупроводнике.

На кривой можно выделить три участка:

         1 – примесной проводимости;

         2 – истощения примеси;

         3 – собственной проводимости.

         Тангенсы углов наклона α и β пропорциональны, соответственно, ширине запрещенной зоны и энергии активации примеси. Если перемножить концентрации электронов и дырок для невырожденного полупроводника, то можно убедиться в справедливости соотношения

,                                               (2.28)

где n_i – концентрация носителей в собственном полупроводнике.

         Выражение (2.28) носит название закона действующих масс. Его можно сформулировать: произведение концентраций электронов и дырок в невырожденном полупроводнике при данной температуре является величиной постоянной и равной квадрату концентраций собственных носителей. Объясняется это тем, что равновесные концентрации устанавливаются в результате двух процессов – генерации и рекомбинации. Когда в зоне проводимости кроме собственных электронов имеется небольшое число примесных электронов, освобождающиеся уровни в валентной зоне гораздо быстрее заполняются электронами , что приводит к резкому уменьшению концентрации дырок.

         ПРИМЕР 3. Положение уровня Ферми в полупроводнике.   [7]

         Определить положение уровня Ферми в германии п – типа при температуре 300 К, если на 10⁶ атомов германия приходится один атом примеси. Концентрация атомов в германии равна 4,4ּ10²³ атомов/м³. Константа в выражении, связывающем число электронов в единице объеме в зоне проводимости с температурой и энергетическими уровнями, равна 4,83ּ10²¹м^-2ּК^-3/2. Ширина запрещенной зоны 0,72 эВ, а расстояние между дном зоны проводимости и донорным уровнем (энергия активации примеси ) 0,01 эВ.

         Решение: поскольку концентрация атомов в германии равна 4,4ּ10²⁸м^-3 и на 10⁶ атомов германия приходится один атом примеси, то число свободных электронов в нем составляет 4,4ּ10²²м^-3. Концентрация свободных электронов в германии определяется в виде:

,

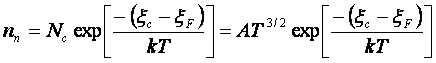
где А=4,83ּ10²¹м^-3ּК^-3/2 – константа, связывающая число электронов в единице объема в зоне проводимости с температурой и энергией уровней,   N_c – эффективная плотности состояний в зоне проводимости, определяемая выражением

.

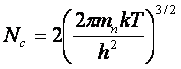         Поскольку энергия активации примеси равна 0,01 эВ, а ширина запрещенной зоны ξ_g=0,72 эВ, можно предположить, что все атомы примесей ионизированы, и пренебречь тепловой генерацией носителей. Тогда можно вычислить величину N_c при заданной температуре Т=300 К. Подставляя в выражение N значение Т^3/2=5196 К, находим, что N_c=4,83ּ10²¹ּ5196=

=25ּ10²⁴м^-3.

         Преобразуем выражение для n_п к виду

,

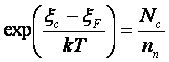или

,

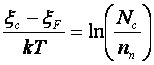отсюда получим

.

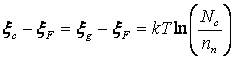         Таким образом,

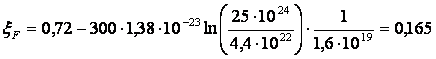 эВ.

Это означает, что уровень Ферми находится на 0,165 эВ ниже дна зоны проводимости.

ПРИМЕР 4. Вывод точечных соотношений для  концентрации носителей в примесных полупроводниках.

         Выведите точное значение для концентрации дырок p_n в полупроводнике n – типа через концентрацию доноров N_Д и собственных носителей n_i. Выведите так же выражение для концентрации электронов в материале р – типа через концентрацию акцепторов N_a и собственных носителей n_i. Считать при этом, что все примеси ионизированны. Определите соотношение N_Д/n_i, если n_n= 1, 005 N_Д.