Легирование атомами бора (III группа) превращает кремний из n-типа в p-тип, так как концентрация акцепторов теперь будет превосходить концентрацию доноров. Результирующая концентрация акцепторов будет, однако, меньше, чем концентрация атомов бора вследствие компенсации донорами. Следовательно, кремний будет иметь проводимость p-типа, а концентрация дырок будет равна результирующей концентрации легирующих примесей:
P=Na(B)-[NД(As)+ NД(P)]=1018-(5·1016+3·1016)=9,2·1017 см-3.
2.4. СТАТИСТИКА НОСИТЕЛЕЙ ЗАРЯДА, УРОВНЕЙ ФЕРМИ
Твердые тела представляют собой системы, состоящие из большого числа микрочастиц. Такие системы подчиняются статистическим закономерностям, основной особенностью которых является их вероятностный характер. Они подразделяются на два класса – вырожденные и не вырожденные. Критерием врожденности является отношение числа частиц в системе к числу энергетических состояний N/G. Если N/G << 1, то система является невырожденной. Если же N/G≥1, то – вырожденной. Невырожденные системы подчиняются классической статистике Максвелла-Больцмана [5]. Вырожденные системы подчиняются квантовой статистике. Вероятность распределения частиц по состояниям определяют статистические функции распределения. Они показывают с какой вероятностью f(E, T) частица будет обладать средней энергией Е при температуре Т.
Невырожденные системы описываются функцией распределения Максвелла-Больцмана:
F(E, T)= exp[(EF – E)/kT], (2.10.)
где k – постоянная Больцмана;
EF – энергия Ферми.
Функции распределения для вырожденных систем зависят от типа частиц. Для фермионов (частиц с полуцелым спином) функция распределения Ферми-Дирака имеет вид:
fф(E, T)= (1+exp((E-EF)/kT))-1. (2.11.)
Для бозонов (частиц с целочисленным спином) функция распределения Бозе-Эйнштейна:
fБ(E, T)= (exp((E-EF)/kT)-1)-1. (2.12.)
При условии
exp((E-EF)/kT)>>1 (2.11.)
(2.11.) и (2.12.) переходят в распределение Максвелла-Больцмана (2.10.). Поэтому условие (2.13) называют условием невырожденности. По своему смыслу энергия (уровень) Ферми соответствует термодинамической точке зрения химическому потенциалу системы. Уровень Ферми – это последний занятый уровень при температуре абсолютного нуля, а при любой другой температуре вероятность нахождения на нем электрона равна 0,5.
![]() ПРИМЕР 2. ПОЛОЖЕНИЕ
УРОВНЯ ФЕРМИ.
ПРИМЕР 2. ПОЛОЖЕНИЕ
УРОВНЯ ФЕРМИ.
Определить на какой высоте (в электронвольтах) от дна зоны проводимости находится уровень Ферми в одновалентном натрии, который содержит 2,53·1028 атомов/м3. Предположим, что плотность энергетических состояний в зоне проводимости определяется соотношением
![]()
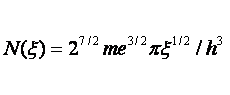 ,
,
![]()
где me – эффективная масса электрона.
Решение:
Умножив N(x) на функцию распределения Ферми – Дирака, наедем действительное число электронов
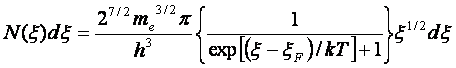
Число электронов в состояниях вплоть до уровня Ферми, можно представить интегралом
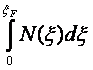 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.