Физические основы микроэлектроники, конспект лекций, страница 12

б) Образование примесной зоны       из примесного уровня                            

         Если принять за критическую концентрацию примеси такое значение , при котором величина энергии Ферми x_F достигает дна зоны проводимости [8], т. е. x_F=x_с, то можно определить соотношение для  в следующем виде:

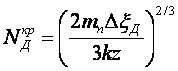,                                       (2.29)

где 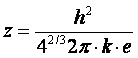, е – основание натурального логарифма.

         Критическая концентрация позволяет границу вырождения, хотя это еще не есть полностью вырожденный полупроводник.

         Вырожденный полупроводник определяют как полупроводник, в котором концентрация носителей заряда не зависит от температуры.

         За критерий вырождения принято [8] условие, состоящее в том, что уровень Ферми в электронном полупроводнике должен располагаться выше дна зоны проводимости не менее чем на 5 кТ, а в дырочном полупроводнике не ниже потолка валентной зоны не менее чем на 5 кТ.

         Концентрация электронов и дырок при этом определяются соотношениями:

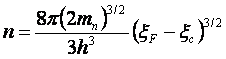,                                      (2.30)

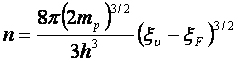.                                    (2.31)

         В металлах электронный газ при любой температуре вплоть до температуры плавления является сильно вырожденным. Концентрация электронов в зоне проводимости определяется соотношением:

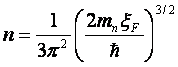.                                       (2.32)

         Уровень Ферми очень слабо зависит от температуры:

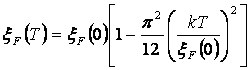,                                  (2.33)

где 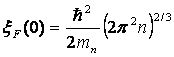 - энергия Ферми при Т=0 К.

         Приведенные соотношения (2.32) и (2.33) справедливы для одновалентных металлов, у которых все валентные электроны частично заполняют лишь одну энергетическую зону. В многовалентных металлах ситуация сложнее, но  там электронный газ является врожденным и его состояние очень мало меняется с температурой.

2.5. ЗАДАЧИ К РАЗДЕЛУ 2

         2.5.1. Привести выражение для вероятности того, что данное энергетическое состояние занято электроном, отдельно в случае распределения Максвелла – Больцмана и распределения Ферми – Дирака. В чем существенное различие между этими функциями распределения и при каких условиях используется каждая из этих функций? Определить температуру, при которой в проводнике вероятность найти электрон с энергией 0,5 эВ над уровнем Ферми равна 2%.

         2.5.2. Дайте краткое объяснение понятий запрещенной зоны и уровня Ферми примечательно к чистому (беспримесному) полупроводнику. Ширина запрещенной зоны чистого полупроводника 1 эВ. Вычислить вероятность заполнения электроном уровня вблизи дна зоны проводимости при  температурах 0 и 290 К соответственно.

         2.5.3. В собственном полупроводнике концентрация электронов проводимости  при температуре 300 К равна 1,5×10¹⁶м^-3. Вычислить ширину запрещенной зоны и энергию уровня Ферми для данного полупроводника. Константа А в выражении, связывающим число электронов проводимости в м³ с температурой и энергией уровней, равна 4,83×10²¹м^-3×К^-3/2.

         2.5.4. Пусть уровень Ферми полупроводника находится на 0,3 эВ ниже дна зоны проводимости. Какова вероятность того, что при комнатной температуре энергетические уровни, расположенные на расстояние 3кТ выше дна зоны проводимости, заняты электронами? Каково вероятность того, что уровень потолка валентной зоны содержит дырки, если ширина валентной зоны 1,1 эВ?