Электротехника \ Физические основы микроэлектроники

Физические основы микроэлектроники, конспект лекций, страница 3

где               - радиус-вектор;

              - волновой вектор;

              А0 - амплитуда волны.

Энергия свободного электрона оказывается непрерывной функцией волнового числа К, т.е. энергетический спектр свободного электрона является сплошным:

E=(h2K2)/2m(2.5.)

Для электрона, движущегося в периодическом поле кристалла, картина становится более сложной.

2.1. ОБОБЩЕСТВЛЕНИЕ ЭЛЕКТРОНОВ В КРИСТАЛЛЕ

В кристалле расстояние между атомами настолько малы, что валентные электроны каждого атома оказываются в достаточно сильном поле соседних атомов. Если в первом приближении считать, что ядра атомов неподвижно закреплены в узлах кристаллической решетки, а энергию попарного взаимодействия каждого электрона с усредненным полем всех остальных, то уравнение Шредингера, для отыскания стационарных состояний, находящегося в кристалле, принимает вид:

                           (2.6.)

где U – потенциальная энергия электрона;

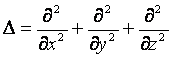                      - оператор Лапласа.

Решение уравнения (2.6.) может быть получено в виде

                (2.7.)

где    , ,  - проекция волнового вектора на оси координат;

          a, b, c         - постоянные решетки в соответствующих направлениях;

         С                -усредненная потенциальная энергия электрона в самосогласованном поле [3];

А      -обменный интеграл, учитывающий энергию обменного взаимодействия;

Eam – энергия некоторого уровня в изолированном атоме.

Обменная энергия обусловлена тем, что каждый электрон может быть с некоторой вероятностью обнаружен у любого атома. Из (2.7.) следует, что в результате взаимодействия атомов, уровень Eam энергии электрона в изолированном атоме опускается на величину С и расщепляется в зону в интервале от

Emin = Eam +C-6|A| до Emin = Eam +C+6|A|,                      (2.8.)

          Эти разрешенные зоны энергии разделены запрещенными энергетическими интервалами – запрещенными зонами.

          Энергетические зоны, образовавшиеся в результате расщепления уровней валентных электронов, называют валентными. Следующая за валентной разрешенная зона называется зоной проводимости.

          На рис. 2.1. показано образование зон при сближении атомов.

 


Число энергетических уровней в хоне является конечным и достаточно большим (число атомов в кристалле). Следовательно, согласно принципу Паули [3] в зоне может разместиться конечное число электронов.

2.2. ЗАПОЛНЕНИЕ ЗОН ЭЛЕКТРОНАМИ И ДЕЛЕНИЕ ТЕЛ НА МЕТАЛЛЫ, ДИЭЛЕКТРИКИ И ПОЛУПРОВОДНИКИ

          При ограниченном числе электронов, содержащихся в твердом теле, заполненными окажутся лишь несколько наиболее низких энергетических зон.

          По характеру заполнения зон электронами все тела можно разделить на две группы.

          К первой группе относят тела, у которых над целиком заполненными зонами расположена зона, заполненная лишь частично. Такая зона возникает в том случае, когда атомный уровень, из которого она образуется, заполнен в атоме не полностью. Частично заполненная зона может образоваться также и вследствие наложения заполненных зон на пустые или частично заполненные. Наличие зоны, заполненной лишь частично, присуще металлам (рис. 2.2а) и тела с такой зонной диаграммой являются проводниками.

Скачать файл