Причём tgb=eд/(2*k) , т.е. пропорционален энергии ионизации примеси.
Таким образом, область ab соответствует примесной проводимости полупроводника, возникающей вследствие ионизации примесных атомов, приводящей к появлению примесных носителей тока.
Область bc простирается от температуры истощения примесей Тs до температуры перехода к собственной проводимости Тi . В этой области все примесные атомы ионизированы, но ещё не происходит заметного возбуждения собсвенных носителей, вследствие чего концентрация носителей тока сохраняется приблизительно постоянной и равной конценрации примеси n=Nд . Поэтому температурная зависимость проводимости полупроводника в этой области определяется зависимостью подвижности носителей. Область cd соответствует переходу к собственной проводимости полупроводника и была рассмотрена ранее.
Резкая зависимость сопротивления полупроводника от температуры ис-пользуется для устройства большого класса полупроводниковых приборов – термосопротивлений или термисторов. Они представляют собой объёмные полупроводниковые сопротиволения с большим температурным коэффициентом сопротивления и нелинейной вольтамперной характеристикой.
Пример 5. Проводимость собственного полупроводника.
Требуется показать, что электропроводность собственного полупроводника определяется выражением:
si = ni*q*(Un+Up) .
Градиент потенциала в образце кремния собственной проводимости составляет 400 В/м, а подвижности электронов и дырок равны 0.12 и 0.025 м2/(В*с) соответственно. Определить для этого образца:
а) скорости дрейфа электронов и дырок;
б) удельное сопротивление кремния, полагая, что концентрация собственных носителей равна 2.5*1016 м-3;
в) полный дрейфовый ток, если площадь поперечного сечения образца
3*10-6 м2.
Покажите также, что проводимость материала n и p-типа определяется приближёнными выражениями:
sn = q*Nд*Nn , sp = q*Na*Up ,
где Nд , Na – концентрации доноров и акцепторов.
Решение: Закон Ома в дифференциальной форме
j = s*Е .
Ток в образце создаётся двумя носителями зарядов – дырками и элекро-нами, т.е. он состоит из двух компонентов дырочной и электронной:
jp = ni*q*Up*E = ni*q*Vдр , jn = ni*q*Un*E = ni*q*Vдn ,
где Vдр , Vдn – скорости дрейфа дырок и электронов соответственно;
Up , Un – подвижности дырок и электронов.
Общая плотность тока запишется в виде:
j = jn+jp = ni*q*E*(Un+Up) .
Скорости дрейфа элекронов и дырок определяются из соотношений:
Vдn = Un*E = 0.12*400 = 48 м/с ,
Vдр = Up*E = 0.025*400 = 10 м/с .
Удельное сопротивление кремния равно:
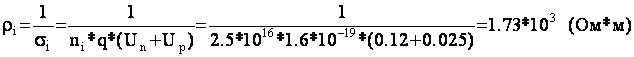 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.