Физические основы микроэлектроники, конспект лекций, страница 29

Распределение электростатического потенциала определяется уравнением Пуассона

 

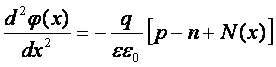                                                                                         (4.2)

где N(x) = - N_a  при  х < 0 и N(х) = N_д  при x > 0

         Для того, чтобы получить простое аналитическое выражение для зависимости φ(x) внутри запорного слоя и ширины запорного слоя, приходится испльзовать следующее приближение. В р-области вводится условная граница запорного слоя в точке (-lp) (рис. 4/1в), правее которой концентрация р,n << N_a, а левее – влияние контакта уже не сказывается и в соответствии с условием квазиэлектронейтральности концентрация дырок равна концентрации акцепторов р ≈ N_a. Электрическое поле в точке  (-lp) настолько мало, что его можно считать равным нулю E (-lp) = 0. Аналогичным образом, в n-области в точке ln вводится условная граница между запорным слоем и квази-нейтральной областью, левее которой         р,n << N_д, а правее – концентрация n ≈ N_д, причем поле E (ln) = 0.

         Так как уровень отсчета потенциала можно выбрать произвольно, причем φ (-lp) = 0. Учитывая, что разность потенциалов на запорном слое составляет Δφ_0,  получим второе граничное условие для потенциала           φ(ln) = Δφ_0.

            Решая уравнение Пуассона для р-области и n-области, получим:

φ₁(х) = Δφ₀ – (qN₀ / 2 εε₀)_* (x + lp)²                             (4.3)

φ₂(х) = (qN_д / 2 εε₀)_* (x + ln)²                              (4.4)

         Выражения для напряженности поля по обе стороны границы раздела будут иметь вид:

E₁(x) = dφ₁/ dx  = - (qN_a / εε₀ ) _* (x + lp)                               (4.5)

E₂(x) = dφ₂/ dx  = (qN_д / εε₀ ) _* (x - ln)                                   (4.6)

         Из условия непрерывности поля на границе раздела E₁(0) = E₂(0) вытекает, что объемные заряды с любой стороны контакта равны между собой

Q = SqN_alp = SqN_д ln,                                          (4.7)

Или

N_д / N_a = lp / ln.                                                      (4.8)

Из (4.8) следует, что симметричный переход имеет одинаковую протяженность в смежных слоях, а несимметричный переход лежит в основном высоком слое.

Из условия непрерывности потенциала φ₁(0) = φ₂(0) получаем выражение для ширины перехода в равновесном состоянии.

L₀ = lp–ln=[2 εε₀ Δφ₀ 1/q(1/N_a+1/N_д)]^½ ,                    (4.9)

            Где, ε₀  - диэлектрическая проницаемость вакуума;

         ε – относительная диэлектрическая проницаемость полупроводника.

         Поскольку  переход является наиболее высокоомной частью структуры, то можно сказать, что подключение к переходу внешнего напряжения изменяет высоту потенциального барьера на величину приложенного напряжения, так как практически все напряжение падает на переходе

Δφ = Δφ₀ ±U;                                      (4.10)

            Знак "-" относится к прямому включению, а "+" к обратному.

         Изменение высоты барьера приводит к изменению ширины перехода и концентрации носителей на границе перехода. Подставляя (4.10) в (4.9) получаем: