Физические основы микроэлектроники, конспект лекций, страница 17

         L = 2.44 * 10^-8  (Вт*Ом*К^-2) называется числом Лоренца.

В полупроводниках с невырожденным электронным газом теплопроводность не является чисто  электронной.  Значительную  долю  в  ней  составляет решёточная теплопроводность.

3.3. Электропроводность полупроводников.

         Как известно, плотность тока j есть заряд, проходящий в  единицу  времени  через единичное поперечное сечение, т.е.

                                     j = q*n*V_д ,                                            (3.18)

где q – заряд электрона; n – концентрация носителей в кристалле; V_д – скорость их перемещения в электрическом поле.

Подставляя сюда выражение (3.3) для V_д ,  и учитывая  закон  Ома j=s*Е ,

получим

                         s = q*n*U_n   .                                           (3.19)

Если  в  кристалле  кроме  электронов  содержатся  и  дырки,  то выражение для удельной проводимости примет вид:

                               s = q*(U_n*n+U_p*p) ,                                       (3.20)

где  U_n – подвижность электронов;

        U_p – подвижность дырок;

         p – концентрация дырок.

         Полупроводники высокой степени очистки обладают электрической проводимостью,  обусловленной  наличием  в  них  собственных  носителей  тока – электронов в зоне проводимости  и  дырок в валентной зоне. Эту проводимость называют  собственной  проводимостью  полупроводника.  Причём, в собственном полупроводнике n = p = n_i .Тогда полная проводимость собственного полупроводника

   s_i  = s_n+s_p  = q*n_i*(U_n+U_p) .                             (3.21)

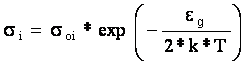         Концентрация электронов и дырок в собственном полупроводнике  определяется выражением (2.22), подвижность – (3.7) и  (3.8). Подставляя эти значения в (3.21), получим

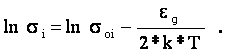где через s_оi обозначено выражение, стоящее перед экспонентой и слабо зависящее от температуры. Выражение (3.22) удобно представлять на графике  в  логарифмическом масштабе:

 

          Зависимость (3.23) представлена на рис.3.3.  Она представляет собой прямую линию, тангенс угла наклона которой  к  оси  абсцисс пропорционален ширине запрещённой зоны e_g : tga = e_g/(2*k). Отрезок, отсекаемый прямой на оси ординат определяет значение  величины  lns_oi .

 

                                            lns_i      

                                            lns_oi