Физические основы микроэлектроники, конспект лекций, страница 2

В зависимости от места расположения частиц в элементарной ячейке могут быть 4 типа кристаллических решеток: примитивная, гранецентрированная, базоцентрированная, объемоцентрированная. Примитивная решетка содержит образующие частицы только в вершинах элементарных ячеек. Гранецентрированная имеет дополнительно по одной частице в центре каждой из ее граней. Базоцентрированная решетка имеет только две дополнительные частицы в центрах оснований. Объемоцентрированная решетка содержит одну дополнительную частицу в точке пересечения пространственных диагоналей.

Всего существуют 14 типов простых кристаллических решеток, которые называют решетками Браве. В зависимости от степени симметрии они подразделяются на семь систем сингоний: триклинная, моноклинная, ромбическая, тетрагональная, тригональная и кубическая. Кроме простых решеток Браве существуют сложные решетки с базисом. Их можно представить себе как систему из двух простых решеток, вставленных одна в другую, и сдвинутых на некоторый вектор, который называют базисом. Подобные решетки имеют Ge, Si и алмаз.

2. ОСНОВНЫЕ ПОНЯТИЯ ЗОННОЙ ТЕОРИИ И СТАТИСТИКА НОСИТЕЛЕЙ ЗАРЯДА В ПОЛУПРОВОДНИКЕ

Любое твердое тело представляет собой совокупность большого числа атомных ядер и электронов, являющихся микрочастицами. Микрочастицы – электроны, протоны, атомы и т.д. – органически сочетают в себе корпускулярные и волновые свойства. Они регистрируются всегда как частицы, а их движение описывается волновым уравнением Шредингера. Для микрочастиц массы m, движущейся в силовом поле и обладающей в нем потенциальной энергией U(x, y, z, t), уравнение Шредингера имеет вид [I,2]

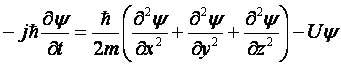                          (2.1.)

Функцию , являющуюся решением этого уравнения, называют волновой функцией. Она имеет следующий физический смысл: произведение на , комплексно сопряженную с , и на объем dV есть вероятность обнаружить частицу в момент t в выделенном элементе объема dV.

         Потенциальная энергия U, входящая в уравнение Шредингера, является в общем случае функцией координат и времени. Однако, для некоторых практических случаев она является функцией только координат и не зависит от времени. В этом случае существует набор независимых решений уравнения Шредингера, для которых не зависит от времени. Такие состояния микрочастицы называются стационарными. Нахождение стационарных энергетических состояний является важной задачей, так как любое другое состояние, в том числе нестационарное, может быть представлено как суперпозиция стационарных состояний. Решение уравнения Шредингера для электрона в кулоновском поле протона (атом водорода) дает бесконечное множество возможных стационарных энергетических состояний. Их энергия, отсчитанная от энергии свободного, не связанного с ядром, электрона, определяется формулой

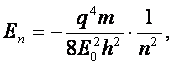                               (2.2.)

где              Е₀ – диэлектрическая проницаемость вакуума;

                   h – постоянная Планка;

                   q, m – заряд и масса электрона;

                   n – главное квантовое число.

Таким образом, электрон, связанный с атомом может принимать лишь строго определенные значения энергии. В этом случае говорят, что энергетический спектр квантован.

         Для свободного электрона уравнение Шредингера принимает вид:

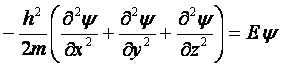                                      (2.3.)

Решением его является плоская волна                            (2.4.)