Физические основы микроэлектроники, конспект лекций, страница 20

         Полный дрейфовый ток:

         Y = n_i*q*(V_дn+V_др)*S = 2.5*10¹⁶*1.6*10^-19*(48+10)*3*10^-6 = 0.696 (мкА)

         Для материала n-типа проводимость определяется выражением:

                                                  s_n = q*(p*U_p+n*U_n)  ,

где n,p – концентрации электронов и дырок .

         Плотность электронного тока в материале n-типа имеет вид:

                                              j_n = n*q*U_n*E + p*q*U_p*E .

         Однако, поскольку n*p=n_i² , а n»N_д имеет N_д*p»n_i² . Поэтому p»n_i²/N_д , и

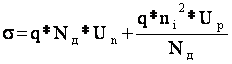следовательно

         Поскольку  в  материале   n-типа  преобладают  электроны,  то  получаем приближённое соотношение

                                                          s_n » q*N_д*U_n .

         Аналогично, для материала p-типа можно получить:

                                                          s_p » q*N_а*U_p .

         Пример 6. Вычисление проводимости примесного полупроводника.

         Дан образец легированного кремния p-типа длиной 5 мм, шириной 2 мм

и толщиной 1 мм.

         Вычислить концентрацию примеси в образце, если электрическое сопротивление образца 100 Ом, подвижность электронов и дырок равна 0.12 и 0.025м²/В*с), а концентрация собственных носителей равна 2.5*10¹⁶ м^-3. Определить также отношение электронной проводимости к дырочной.

         Решение:

         Используя основную формулу для удельного сопротивления, получаем:

Удельное сопротивление определяется также выражением:

         Подставляем в это выражение числовые данные из условия задачи:

p*0.025+n*0.12 = 1.56*10²⁰ .

         Используя закон действующих масс p*n=n_i², находим n=6.25*10³²/p и подставляем в соотношение, полученное ранее:

0.025*p²+0.12*6.25*10³²-1.56*10²⁰*p=0 .

Решение уравнения даёт результат p=6.24*10²¹ м^-3.

Отношение электронной проводимости к дырочной получим из соотношения:

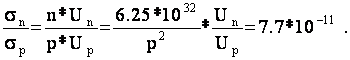Удельное сопротивление определяется также выражением :

 

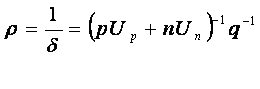Подставляем в это выражение числовые данные из условия задачи  :