Физические основы микроэлектроники, конспект лекций, страница 41

Рис. 4.10. Зонные диаграммы полупроводника при наличии поверхностных                             

                 состояний:

                 а) режим обогащения;  б) обеднение;

                 в) инверсия

  Независимо от типа проводимости материала зоны будут изогнуты вниз при положительном заряде на поверхности, вверх - при отрицательном. Обычно изгиб зон измеряется разностью энергий середины запрещенной зоны (пунктирная линия на рисунке 4.10.) в приповерхностной зоне и в глубине кристалла.

  Толщина приповерхностного слоя, где происходит изгиб зон определяется объёмными характеристиками кристалла. Её полагают равной Дебайевской длине экранирования

L_D=(εε₀φ_T/2qn₀)^1/2                                        (4.47)

где n₀ – концентрация носителей заряда в глубине кристалла.

  Концентрация носителей заряда в приповерхностном слое зависит от координаты и определяется соотношениями:

n=n₀exp(qφ(x)/kT), p=p₀exp(qφ(x)/kT)                    (4.48)

где n₀ и p₀ – концентрации носителей в объёме;

        φ(x)   - потенциал.

  В зависимости от знака и величины заряда на поверхности могут возникнуть три режима: а) обогащение, б)обеднение, в) инверсия (рис. 4.10). Первый режим соответствует тому, что концентрация основных носителей больше в приповерхностном слое чем в глубине образца. Второй режим говорит об обратном соотношении. Инверсией называют режим, когда приповерхностный слой меняет тип проводимости и противоположный. Это возможно при сильном обеднении. На рис. 4.10,в видно, что уровень электростатического потенциала (средина запрещенной зоны) пересекает в точке А уровень Ферми.

  Точка А характеризуется собственной проводимостью. В слое отсечения, проходящего через точку А, до поверхности, концентрация не основных носителей превышает концентрацию основных, а это равносильно изменению типа проводимости.

   Значение потенциала можно определить из решения уравнения Пуассона для приповерхностного слоя при соответствующих граничных условиях.

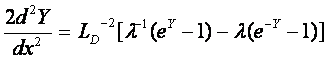                          (4.49)

где Y=φ/φ_T   – безразмерный потенциал;

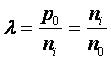          - степень легирования.

Граничные условия: Y=Ys при x=0 и 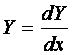  при x→∞.

  Решение уравнения Пуассона имеет вид:

dY/dx=L_D^-1F(Y,λ)                                          (4.50)

где F(Y,λ)=[λ(e^-Y-1)-λ^-1(1-e^Y)+Y(λ-λ^-1)]^1/2.       

  Полный заряд в приповерхностной области определяется как

Qs=2qn_iL_DF(Y,λ)                                              (4.51)

Поверхностная проводимость может быть определена из соотношения

σ_S=q(ΔnU_n+ ΔpU_p)=qU_pn_iL_Dg                                  (4.52)

где     ,

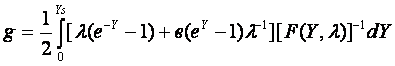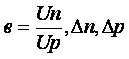           - изменения концентрации носителей вблизи поверхности.

  График функции σ_S(Y_S) приведен на рис. 4.11.

 

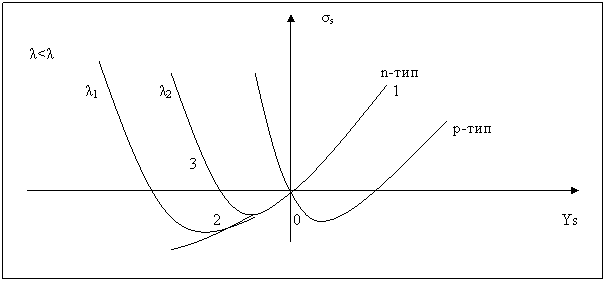  Рис. 4.11.   Зависимость поверхностной проводимости от изгиба зон.

  При положительном значении Ys  (изгиб зон вниз) σ_s растет из-за наличия обогащенного слоя у поверхности полупроводника n- типа (ветвь 1).