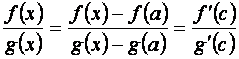 ,
,
где a< c< x. Тогда, очевидно, если x® a, то и c® a, поэтому из предыдущего равенства имеем:
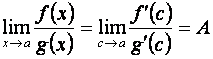 .
.
Теорема доказана.
Таким образом, доказанное правило Лопиталя, сводит предел отношения функций к пределу отношений производных, если последний существует. Часто оказывается, что нахождение предела отношения производных проще и его можно найти элементарными способами.
Найдем несколько пределов с помощью доказанной теоремы.
1. Найти предел: 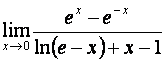
Нетрудно
видеть, что ![]() и
и ![]() , т. е. мы имеем неопределенность
вида
, т. е. мы имеем неопределенность
вида ![]() . Можно воспользоваться
правилом Лопиталя, согласно которому искомый предел равен пределу отношения
производных. Таким образом, получаем:
. Можно воспользоваться
правилом Лопиталя, согласно которому искомый предел равен пределу отношения
производных. Таким образом, получаем: 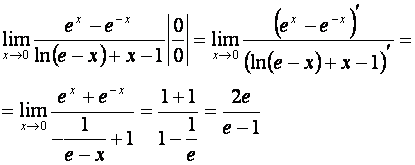
2. Найти предел:
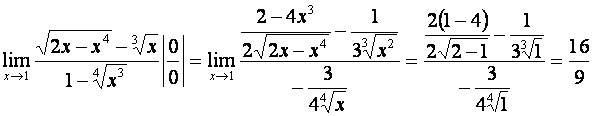
3. Найти предел:
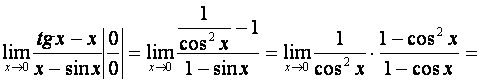
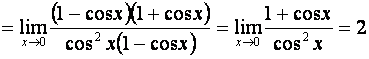 .
.
Замечание
1. Иногда правило Лопиталя нужно применять несколько раз. Это необходимо в
том случае, когда после применения правила Лопиталя неопределенность ![]() остается. В качестве примера
рассмотрим вычисление следующего предела.
остается. В качестве примера
рассмотрим вычисление следующего предела.
4. Найти предел:
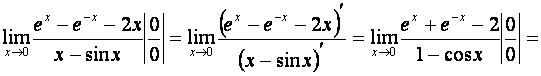
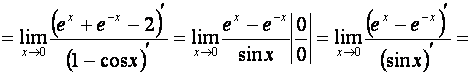
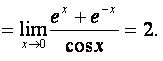
Замечание
2. Правило Лопиталя можно применять и в том случае, когда аргумент х
стремится не к конечному числу, а к бесконечности, т.е. если ![]() функции f (x) и g
(x) дифференцируемы на промежутке (a, +¥) , то имеет место равенство:
функции f (x) и g
(x) дифференцируемы на промежутке (a, +¥) , то имеет место равенство:
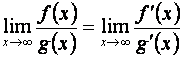
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.