Исследование функций. Приложение производной, страница 8

Если взять только один член в разложении, то есть , то для того, чтобы погрешность была меньше , достаточно взять 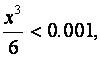 ( x> 0)  или x < 0.1817, что соответствует примерно . Если использовать два члена формулы, т. е. 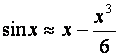, то для достижения той же точности уже достаточно взять 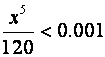 или .

Таким образом, с увеличением числа членов многочлена Тейлора, он с все большей точностью и на большом протяжении воспроизводит исходную функцию.

5.Правило Лопиталя. Семь видов неопределенностей и их раскрытие.

5.1. Неопределённость вида . (Правило  Лопиталя).

Если  = 0, то при вычислении предела отношения этих функций мы имеем неопределенность вида . Для вычисления пределов такого рода полезно нижеследующее утверждение, называемое правилом Лопиталя.

Теорема. Если функции f (x) и g (x)  определены в промежутке (a, b) и , , кроме того, пусть в промежутке(a, b) существуют конечные производные f¢ (x) и    g¢ (x), причем g¢ (x) ¹ 0, и существует предел 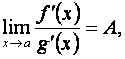 то имеет место равенство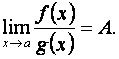  

Доказательство. Функции f (x) и g (x) доопределим в точке x= a по непрерывности, положив f (a) = f (b) = 0. Тогда эти функции непрерывны на замкнутом промежутке [a, b]. Применяя теорему Коши, получим: