Исследование функций. Приложение производной, страница 11

Таким образом, показательная функция с основанием больше единицы возрастает быстрее степенной функции.

7. Найти предел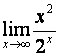     

.

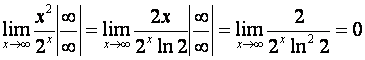5.3. Неопределенность вида

Если  а  то при вычислении предела  мы имеем дело с неопределенностью вида  0×¥.  Неопределенность такого типа легко привести либо к неопределенности вида , либо к неопределенности вида , а затем воспользоваться правилом Лопиталя. В самом деле:

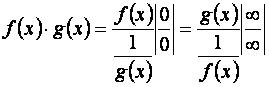
8. Найти предел:

.

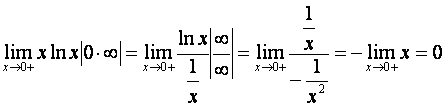5.4. Неопределённость вида

Если при вычислении предела  имеют место равенства  и , то говорят о неопределенности вида . Можно произвести преобразования, сводящие это выражение к неопределенности вида  или :

.

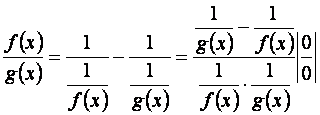Иногда того же результата можно достичь значительно проще.

9. Найти предел:

.

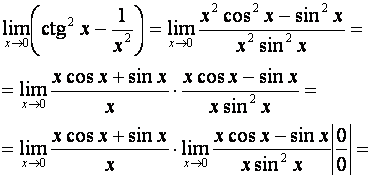
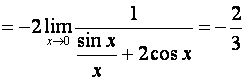5.5. Неопределенности вида

В случае неопределенностей вида  рекомендуется эти выражения сначала прологарифмировать.

Пусть y= [f (x)] ^{g (y)}, тогда ln y= g (x)× ln f (x). Предел ln y  представляет неопределенность вида 0×¥, которую мы изучили ранее. Предположим, что используя приемы, описанные выше, мы нашли , который оказался равный либо конечному числу A, либо +¥, либо -¥. Тогда , соответственно будет либо e ^A, либо +¥, либо 0.