Исследование функций. Приложение производной, страница 20

Отсюда видно, что при переходе через точку x=-3 производная не меняет знака, а при переходе через точку x=3 знак производной меняется с “-” на “+”.

Точка x=-1 не является точкой максимума, потому что в этой точке функция не определена.

Пример 3. Найти экстремум функции

Находим производную функции:

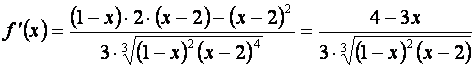
При 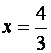 производная равна нулю, а при x=1 и x=2 производная не существует, следовательно, точки x=1, 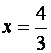, x=2 стационарные точки функции. При переходе через точку x=1 производная не меняет знака и, следовательно, эта точка не является точкой экстремума.

При переходе через точку 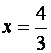 производная меняет знак минус на плюс, следовательно, в точке 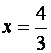 функция имеет минимум. При переходе через точку x=2 производная меняет знак с “+” на ”-“, т. е. точка x=2 - точка максимума. Минимум функции равен 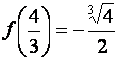, а максимум равен f (2) = 0.

8.3 Наибольшее и наименьшее значение функции.

Согласно теореме Вейерштрасса, всякая непрерывная на отрезке функция достигает на нем своего наибольшего и наименьшего значения. Алгоритм нахождения наибольшего и наименьшего значения функции состоит в следующем.

Пусть f (x) непрерывна на отрезке [a, b] и имеет на нем к стационарных точек . Тогда наибольшее значение функции  f (x) на отрезке [a, b] равно наибольшему из чисел f (a),  f (x₁),…f (x_k), f (b), а наименьшее значение функции f (x) - наименьшему из этих чисел.

Пример 4. Найти наибольшее и наименьшее значения функции

f (x) = 2x³- 3x²- 36x- 8на отрезке [-3, 6].

Находим производную функции:  f¢(x) = 6 (x+2) (x-3) .