При переходе через точку x= 3 производная меняет знак “-” на “+”, следовательно, в этой точке функция имеет минимум. Вычислив значения функции в точках x= 2 и x= 3, найдем экстремумы функции: максимум f (2)= 14 и минимум f (3)= 13.
Тот же
результат можно получить, используя вторую производную. Так как f² (x) = 12x -30, то f² (2) = -6 < 0, а ![]() ,
то в точке x= 2 функция
имеет максимум, а при x=3
- минимум.
,
то в точке x= 2 функция
имеет максимум, а при x=3
- минимум.
Пример 2. Найти экстремумы
функции 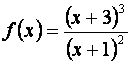
Найдем производную этой функции:
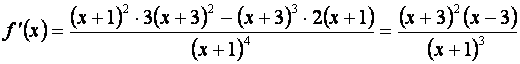
Стационарные точки функции x=-3 и x=3.
Точка x=-1 не является стационарной, потому
что при x=-1 функция не определена. Легко
видеть, что при переходе через точку x=-3
производная не меняет знака, следовательно, точка x=-3 не
является точкой экстремума. В точке x=3 производная меняет знак с “-” на “+”, следовательно, в этой точке минимум. Находим 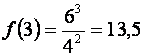 .
.
Замечание. Для определения
знака производной достаточно решить неравенство 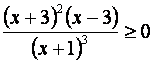 .
.
Это неравенство решается методом интервалов:
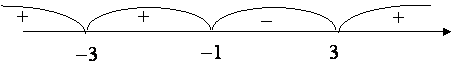 |
|
|
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.