Таким образом, y = x -1- наклонная асимптота.
Пример 2.Найти все асимптоты графика функции
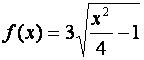 .
.
Функция
определена и непрерывна при ![]() , следовательно, вертикальных
асимптот нет. Функция четная. Найдем
асимптоты при
, следовательно, вертикальных
асимптот нет. Функция четная. Найдем
асимптоты при ![]() ,
используя формулы (10.3),(10.4).
,
используя формулы (10.3),(10.4).

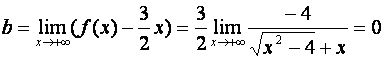
Таким образом, прямая 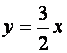 -
наклонная асимптота. Исследуем поведение функции при
-
наклонная асимптота. Исследуем поведение функции при ![]()
![]() .
.

Несложно
показать, что и в этом случае ![]() .
Следовательно,
.
Следовательно, 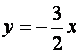 - также асимптота графика функции.
- также асимптота графика функции.
11. Построение графиков
Все исследования, проведенные выше, нужны, в основном, при построении графиков функций. В ходе построения графиков функций можно придерживаться, например, следующей схемы:
1. Найти область определения функции. Проверить, является ли функция четной, нечетной, периодической.
Найти точки пересечения графика с осями координат, промежутки, где значения функции положительны, отрицательны. Найти точки разрыва функции.
2. Найти асимптоты графика. Найти односторонние пределы функции в граничных точках области определения и в точках разрыва.
3. Вычислить первую производную функции, найти экстремумы и промежутки ее возрастания и убывания.
4. Вычислить вторую производную, найти точки перегиба графика, промежутки выпуклости и вогнутости графика функции.
5. Нарисовать график функции.
При решении конкретной задачи отдельные этапы этой схемы могут быть расширены, другие же могут быть совершенно излишними.
Рассмотрим несколько примеров построения графиков функций.
Пример 1.Построить
график функции 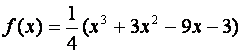 .
Данная функция определена на всей числовой прямой и бесконечное число раз
дифференцируема. Так как
.
Данная функция определена на всей числовой прямой и бесконечное число раз
дифференцируема. Так как ![]() , то асимптот нет. График пересекает ось ординат в точке
, то асимптот нет. График пересекает ось ординат в точке 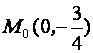 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.