если существует предел, стоящий справа.
5.2. Неопределенность типа ![]()
Если ![]() и
и ![]() , то при вычислении предела отношения
этих функций мы имеем дело с неопределенностью вида
, то при вычислении предела отношения
этих функций мы имеем дело с неопределенностью вида ![]() . Заметим, что здесь
. Заметим, что здесь ![]() может быть как конечным числом, так
и бесконечностью. Для вычисления этих пределов справедливо то же правило
Лопиталя, которое мы приведем без доказательства.
может быть как конечным числом, так
и бесконечностью. Для вычисления этих пределов справедливо то же правило
Лопиталя, которое мы приведем без доказательства.
Теорема. Если
функции f (x) и g (x) определены и дифференцируемы на
промежутке [a, b], g¢ (x)¹ 0
и ![]() ,
, ![]() и если существует предел отношения
производных, т. е.
и если существует предел отношения
производных, т. е. 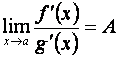 ,
то существует
,
то существует 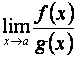 и
он также равен A.
и
он также равен A.
Теорема
остается справедливой и в том случае, когда ![]() стремится к бесконечности.
стремится к бесконечности.
Рассмотрим некоторые примеры.
5. Найти предел
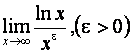
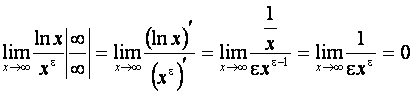
Отсюда в частности следует, что функция g (x)= xe , при любом положительном e стремится к бесконечности быстрее, чем функция f (x)= ln x, т. е. функция логарифм возрастает медленнее, чем любая степенная функция.
6. Найти предел 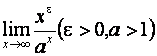
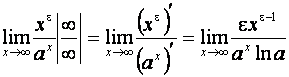 .
.
Если ![]() , то справа имеем неопределенность
того же типа
, то справа имеем неопределенность
того же типа ![]() , но продолжая
этот процесс, используя то же правило Лопиталя, в конце концов, получим степень
с отрицательным или нулевым показателем. Поэтому всегда
, но продолжая
этот процесс, используя то же правило Лопиталя, в конце концов, получим степень
с отрицательным или нулевым показателем. Поэтому всегда 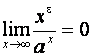 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.