Исследование функций. Приложение производной, страница 6

                                      r_n (x) = f (x) - P_n (x).                                  (5.14)

Отсюда получаем:

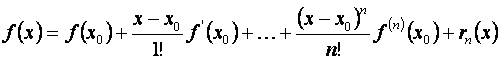.     (5.15)

Равенство (5.15) называют формулой Тейлора для функции f (x) в точке x₀. При этом r_n (x) называют остаточным членом формулы Тейлора. Остаточный член формулы Тейлора можно записать в нескольких видах. Приведём некоторые из них:

1.Форма Пеано:                   .

2.Форма Лагранжа: 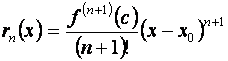            .           (5.16)

c находится между  x₀ и x.

Если  , то формула Тейлора   принимает вид:

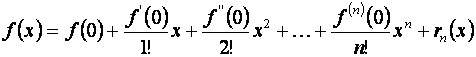          (5.17)

и называется формулой Маклорена. Остаточный член в формуле Маклорена можно вычислить, используя равенства (5.16). Приведём формулы Тейлора для основных функций. Представление функции формулой Тейлора назовём разложением функции по формуле Тейлора.

Разложение элементарных функций.

1.  

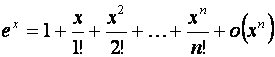
2. 

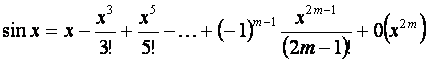
3. 

4.   

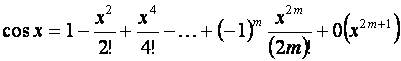
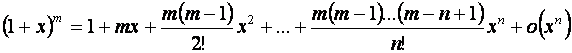
В частности, при 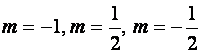 получаем:

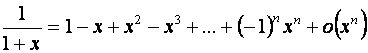
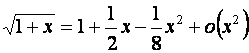
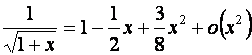
5.