Исследование функций. Приложение производной, страница 3

Геометрическая интерпретация теоремы Лагранжа.

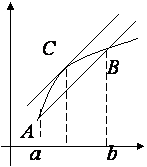Рассмотрим график функции y= f (x) на отрезке [a, b]. Пусть точка A – точка с координатами (a, f (a)) и точка B с координатами (b, f (b)). Проведём секущую AB. Тогда, согласно равенству (5.3), касательная параллельна секущей AB. Этот факт и является геометрической интерпретацией теоремы Лагранжа.

Следствие1 теоремы Лагранжа.

Если производная функции равна нулю в каждой точке некоторого промежутка, то функция постоянна на этом промежутке.

Доказательство. Пусть x – произвольная точка отрезка [a, b]. Согласно теореме Лагранжа имеет место равенство:

                   f (x)- f (a)= f¢ (c)× (x-a).                                             (5.4)

По условию f¢ (x)= 0, следовательно, f (x)= f (a), а это и означает, что f (x) во всех точках x равна значению функции в точке a, т.е.   f (x) постоянна на отрезке [a, b]. Следствие доказано.

Следствие2теоремы Лагранжа.

Если две дифференцируемые функции имеют равные производные на отрезке [a, b], то эти функции отличаются на этом промежутке не более, чем на постоянное слагаемое.

Доказательство. По условию следствия f¢ (x)= g¢ (x), когда х принадлежит отрезку [a, b], т.е. f¢ (x)- g¢ (x)= [ f (x)- g (x)]¢= 0. Таким образом, производная функции f (x)- g (x) на отрезке (a, b) равна нулю и, следовательно, по следствию 1 эта разность равна постоянной величине, т.е. f (x)- g (x)= c.

Следствие доказано.

3.Теорема Коши.

При вычислении пределов мы будем использовать правило Лопиталя, которое докажем ниже. Доказательство этого правила опирается на теорему Коши, которая имеет следующий вид.