Исследование функций. Приложение производной, страница 5

                                      (5.8)

такой, что значение функции f (x) и многочлена P_n (x), а также все производные до –ой включительно функции f (x) и многочлена P_n (x) в точке x₀ совпадают. Другими словами выполняются равенства:

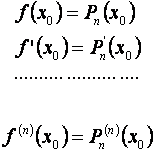
                                                                         (5.9)

Используя равенства (5.9), найдём коэффициенты A₀, A₁, …, A_n многочлена P_n (x), определяемого соотношением (5.8). Из первого равенства (5.9) получаем:

                                                f (x₀) = A₀.                                        (5.10)

Так как

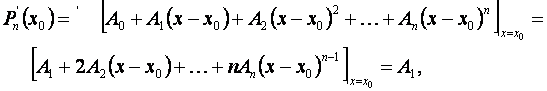
то из второго равенства (5.9) имеем:

                                                A₁ = f¢ (x₀).                                       (5.11)

Аналогично получаем:

                                       .        

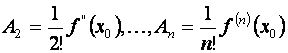Используя равенства (5.10), (5.11), (5.12), многочлен (5.8) можно записать следующим образом:

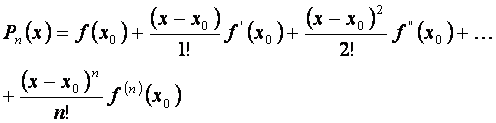      (5.13)

Значения функции f (x) и n её производных в точке x₀ равны соответственно значению многочлена, определённого равенством (5.13) и его производными в точке x₀. Многочлен P_n (x), определённый равенством (5.13), называют многочленом Тейлора.

Совершенно очевидно, что нельзя утверждать равенство       f (x)= P_n (x). Многочлен P_n (x) даёт лишь некоторое приближение функции f (x). Разность между функцией и её многочленом Тейлора обозначим r_n (x), т.е.