Исследование функций. Приложение производной, страница 25

Так как разность ординат ½y -Y½ лишь постоянным множителем (равным косинусу угла между асимптотой и осью x ) отличается от расстояния , то при x®+¥ одновременно с  должна стремится к нулю и эта разность, т.е.

                                                (10.2)

Разделив (10.2) на , получаем

.

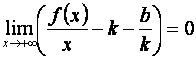Используя свойства пределов (предел суммы равен сумме пределов), окончательно получаем:

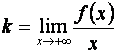                                                     (10.3)

Сейчас, непосредственно из (10.2), получаем

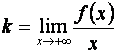                                                     (10.4)

Таким образом, если кривая графика функции y = f (x) имеет наклонную асимптоту Y= f (x)= kx+b, то коэффициенты этой прямой k и b находятся по формулам (10.3) и (10.4) соответственно.

В частности, при  получаем горизонтальную асимптоту, уравнение которой определяется равенством , где

                                                      (10.5)

Для нахождения всех наклонных асимптот графика функции y = f (x) следует отдельно найти асимптоты при  x®+¥   и при   x® -¥.

Пример 1.Найти все асимптоты графика функции .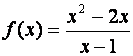

Функция определена и непрерывна всюду, за исключением , и

.

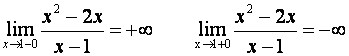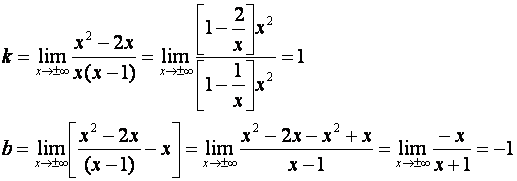
Следовательно, - вертикальная асимптота. Для нахождения наклонных асимптот воспользуемся формулами (10.3),(10.4).