Исследование функций. Приложение производной, страница 29

Пример 2.Построить график функции .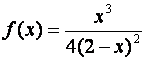

Функция определена на всей действительной оси за исключением точки x= 2. График ее пересекает оси координат в одной точке M (0; 0). Функция положительна при x> 0, x¹ 2 и отрицательна при . Так как , то прямая  x= 2 - вертикальная асимптота графика. Найдем наклонные асимптоты:

.

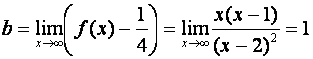
Итак, график имеет наклонную асимптоту .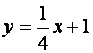

Вычислим первую производную: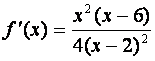      

Отсюда точка x=2 экстремум функции. На интервалах функция возрастает, на интервале  убывает. Следовательно, точка x= 6 - точка минимума и .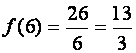

Вычисляем вторую производную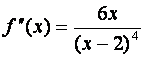

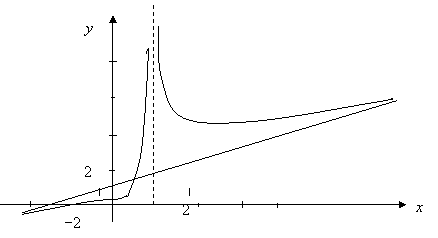
Отсюда следует, что функция имеет единственную точку перегиба при x= 0. Если x< 0 ,то функция выпукла вверх, поэтому ее график при x® -¥ приближается к асимптоте снизу. При         0 < < 2 и при x > 2  функция выпукла вниз. Отсюда следует, что при x® +¥ график приближается к асимптоте сверху. Вычислив еще несколько точек графика, на основе проведенных исследований  делаем рисунок  графика функции.