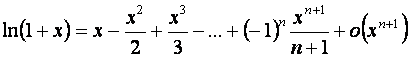
6. ![]()
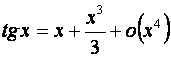
7. ![]()

Применение формулы Тейлора для приближенных вычислений.
Рассмотрим формулу Тейлора
(Маклорена) ![]() с остаточным членом в форме Лагранжа, где вместо c
будем писать qx, 0<q<1. Тогда эта формула будет иметь вид:
с остаточным членом в форме Лагранжа, где вместо c
будем писать qx, 0<q<1. Тогда эта формула будет иметь вид:
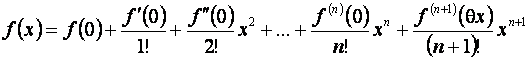 .(5.17)
.(5.17)
Если в формуле (5.17) отбросить остаточный член, то получится приближенная формула:
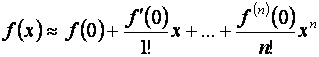 ,
,
заменяющая функцию сложной
природы многочленом. Сейчас мы можем оценить погрешность этой формулы.
Погрешность по абсолютной величине равна отброшенному члену. В частности, если ![]() -я производная ограничена по
абсолютной величине числом
-я производная ограничена по
абсолютной величине числом ![]()
![]() , то
, то 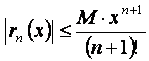 .
.
Если ![]() , то приближенная формула здесь имеет
вид:
, то приближенная формула здесь имеет
вид:
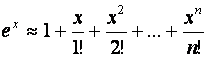
и остаточный член rn (x) в этом случае определяется равенством: 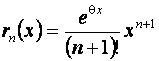 .
.
Таким образом, при x> 0 погрешность оценивается так:
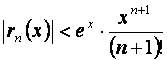 .
.
Для x= 1 имеем:
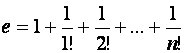 ;
; 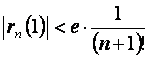 .
.
Если ![]() , то
, то
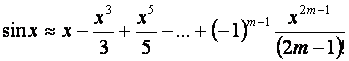 .
.
Остаточный член в этом случае имеет вид:
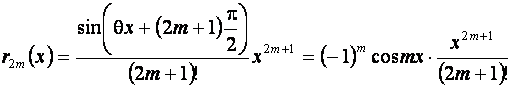
и погрешность оценивается легко: 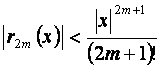 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.