Исследование функций. Приложение производной, страница 2

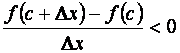
и, следовательно, f¢ (c)£ 0. Отсюда вытекает, что f¢ (c)= 0. Теорема доказана.

Геометрическая интерпретация теоремы Ролля.

Как хорошо известно, значение производной в точке равно значению тангенса угла наклона между касательной, проведённой к графику функции в данной точке и положительным направлением оси OX . В условиях теоремы существует точка, принадлежащая интервалу, в которой производная равна нулю и, следовательно, в этой точке касательная параллельна оси OX .

2. Теорема Лагранжа (о конечном приращении).

Теорема. Если функция y= f (x) непрерывна на отрезке [a, b] и дифференцируема в интервале (a, b), то существует точка c, принадлежащая интервалу (a, b), такая, что выполняется неравенство:

                                      f (b)- f (a)= f¢ (c)× ( b-a ).

Доказательство. Рассмотрим вспомогательную функцию F (x), определённую следующим образом:

                             .

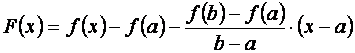Функция F (x) непрерывна на отрезке [a, b], и дифференцируема на интервале (a, b). На концах отрезка функция F (x) принимает равные значения. В самом деле

                             ,

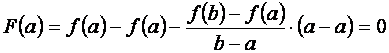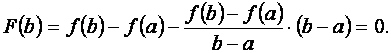
Таким образом, функция F (x) удовлетворяет всем условиям теоремы Ролля, следовательно, существует точка c, в которой     F¢ (c)= 0. Найдём производную функции F (x):

.

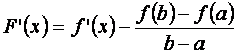Отсюда

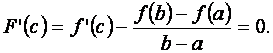
Таким образом,

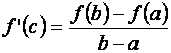                             .                                          (5.3)

Из соотношения (5.3) и вытекает справедливость теоремы.