Исследование функций. Приложение производной

 Исследование функций.

Приложение производной

1. Теорема Ролля.

Многие приложения производной основаны на теореме Лагранжа о конечных приращениях функции, которая будет доказана ниже. При доказательстве теоремы Лагранжа используется теорема Ролля о нуле производной, которая формулируется следующим образом:

Теорема. Пусть функция y= f (x) определена и непрерывна на отрезке [a, b] и дифференцируема на интервале (a, b), тогда, если на концах отрезка функция принимает равные значения, то существует точка c, принадлежащая (a, b), в которой производная функции  f (x) равна нулю , т. е. f¢ (c)=0.

Доказательство.  Так как функция f (x) непрерывна на отрезке [a,b], то она достигает на этом отрезке своего наибольшего и наименьшего значения, которые обозначим соответственно M  и m. При этом возможны два случая: M= m или M и m не равны.

1) если M= m, то y= f (x) – постоянная величина, следовательно, f¢ (x)= 0 во всех точках отрезка [a,b], следовательно, в качестве точки c можно взять любую точку из интервала (a, b).

2) если M и m не равны, то функция y= f (x) не является постоянной. Согласно условию теоремы f (a)= f (b), поэтому хотя бы одно из значений M или m функция принимает во внутренней точке интервала (a, b). Не уменьшая общности, можно предположить, что f (c)= m, где a< c< b. Найдём производную функции  f (x) в точке c. По определению

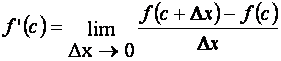.                    (5.1)

При любом значении  всегда выполняется неравенство

          f (c+Dx)- f (c )>0,(5.2)

так как в точке a= c функция  f (x) достигает своего минимума.

Если Dx > 0,  то

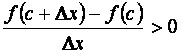
и, следовательно, согласно (5.1),  f¢ (c)³0. Если же Dx < 0, то