Теорема. Если функции f (x) и g (x) непрерывны на отрезке [a, b] и дифференцируемы в интервале (a,b) и, кроме того, производная функции g (x) во всех точках интервала (a, b) отлична от нуля, то существует точка c, принадлежащая интервалу (a,b), такая, что имеет место равенство:
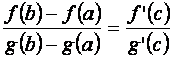. (5.5)
Доказательство. Прежде всего, установим, что g (b)- g (a)¹ 0. В самом деле, по теореме Лагранжа имеет место равенство:
g (b)- g (a)= g' (c)× ( b-a ). (5.6)
По условию теоремы g¢ (c)¹ 0 и, следовательно, правая часть (5.6), равная g¢ (c)× (b-a) отлична от нуля, т.е. g (b)- g (a)¹ 0. Для доказательства справедливости равенства (5.5), как и при доказательстве теоремы Лагранжа, введём вспомогательную функцию F (x), определяемую равенством:
.
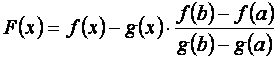(5.7)
Функция F (x) непрерывна на отрезке [a, b] и дифференцируема в интервале (a, b). Вычислим значение функции на концах этого отрезка:
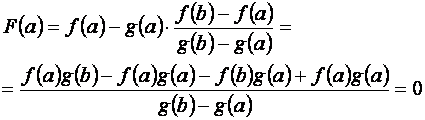
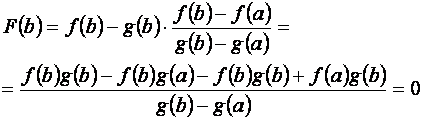
Итак, F (a)= F (b)=0.
Следовательно, функция F(x)
удовлетворяет условиям теоремы Ролля,
согласно которой найдётся точка c, принадлежащая интервалу (a, b), такая, что F¢ (c)= 0. Используя равенство 
,
получаем:
.
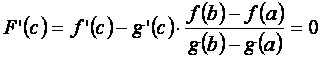Отсюда получаем:
.
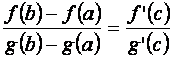Теорема доказана.
4.Формула Тейлора
При вычислении производных, значений функции в точке мы видим, что наиболее просто эти значения вычисляются у многочлена. В силу этого, спрашивается, можно ли заменить функцию многочленом, по крайней мере, в некоторой окрестности заданной точки. Если такая замена возможна, то каким условиям должна удовлетворять функция. Ответы на поставленные вопросы даёт формула Тейлора, которую мы рассмотрим в этом параграфе. Пусть функция f (x), заданная на отрезке [a, b], имеет в каждой внутренней точке этого отрезка (n+1) – производную. Для этой функции найдём многочлен:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.