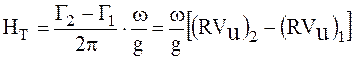Відповіді на екзаменаційні питання № 1-88 дисципліни "Гідродинамічні машини і передачі" (Основне рівняння лопатевих гідромашин. Режими роботи гідродинамічної передачі), страница 2

,  (1)    где       .

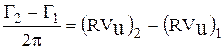Из уравнения оборотных гратов путем превращения получим.

Подставим к уравнению теоретического напора лопастных машин   и имеем

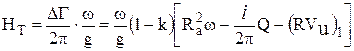
За уравнением (18) решетки для насоса можно построить теоретический напор насоса , если определить коэффициент прозрачности к , коэффициент нулевого направления  и активный радиус  решетки.

Для некоторых случаев плоских решеток (прямая решетка из тонких дужек и колова логаріфмічна решетка с постоянным углом С.С. Руднев дал расчетное определение   . Таким образом, на базе теории решеток дано точное решение для логарифмической лопасти, которая размещена между параллельными дисками.

Коэффициент прозрачности к является функцией трех параметров 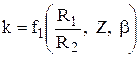Эти параметры можно объединить и привести до двух: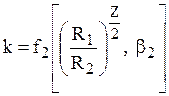Высчитаем коэффициент прозрачности к для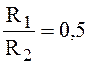 ; Z=8; . Из черт. 7, в видно, что в большинстве практических случаев коэффициентом к можно пренебрегать. Коэффициент к нужно учесть при расчете насосов с малым количеством лопастей.

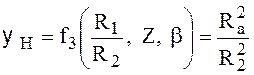.Для частного случая 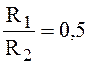; Z=8; , .Для густых решеток  с лопастями, в которых, можно учесть поправку только на активный радиус, потому что в этом случае коэффициент прозрачности k=0. Можно сравнить уравнение ( 1) с теоретическим напором , в котором использован учет конечного количества лопастей по схеме Стодола-Майзеля

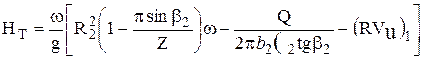 где - коэффициент сжатия;  - ширина межлопастного канала на выходе.

Тогда k=0; 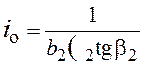     За Пфлейдерером значения теоретического напора

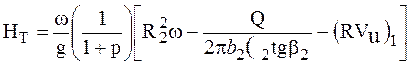 При сравнении с уравнением теоретического напора (1)

;             

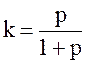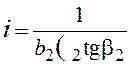
4. Плани швидкостей

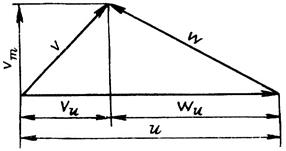Рух рідини у лопатевому колесі можна розглядати відносно нерухомої системи вісей, яка зв’язана з корпусом насоса, відносно рухомої системи вісей, яка зв’зана з колесом, і разом з рухомою системою вісей. Рух рідини у системі нерухомих вісей є абсолютним рухом, рух рідини по відношенню до рухомих вісей – відносним рухом і рух рідини разом із рухомими вісями відносно нерухомих вісей – переносним. У переносному русі рідина обертається навкруги вісі лопатевого колеса з кутовою швидкості , яка дорівнює кутовій швидкості обертання колеса. Абсолютний рух рідини можна розглядати як результат додавання відносного і переносного рухів. Швидкість абсолютного руху V рідини дорівнює геометричній сумі відносної W і колової (переносної) швидкостей:

,                                  

де  (R – радіус розташування точки, в якій визначається план швидкостей).

При геометричному підсумовуванні швидкості утворюють трикутник швидкостей (рис. 1).

Із плана (трикутника) швидкостей маємо

,                                         (2)

де  - колова складова абсолютної швидкості.

В області лопатевого колеса усталеним є тільки відносний рух потоку, який підкоряється рівнянню енергії Бернуллі. Для ідеальної рідини

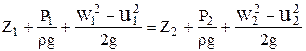
де Z – питома    енергія       розташування;  P  – тиск; індекси “1” і “2” – відповідно вхід до лопатевого колеса  і  вихід  із  нього;        -   густина;  g – прискорення вільного падіння.

З урахуванням формул (2) і (18) можна отримати рівняння для визначення теоретичного напору насоса, яке називають основним рівнянням роботи насоса.

.                         

Теоретичний напір насоса зв’язаний із дійсним напором H за допомогою гідравлічного коефіцієнта корисної дії :

.                                                    

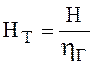Рівняння (4) є справедливим тільки уздовж лінії течії. При переході до течії у всьому каналі потрібно виконати осереднення параметрів потоку у ньому, що практично можливо тільки на розрахунковому режімі роботи лопатевого колеса.

В насосах, як правило, =0. Відповідно  .

5. Коефіцієнт швидкохідності

Для  характеристики   форми  проточної  частини   насосів у відповідності із заданими параметрами, а також для порівняння між собою насосів різних типів, використовують поняття про коефіцієнт швидкохідності, який чисельно рівний частоті обертання робочого колеса насоса даної масштабної серії і розвиває напір 1 м при подачі 0,075 :