Відповіді на екзаменаційні питання № 1-88 дисципліни "Гідродинамічні машини і передачі" (Основне рівняння лопатевих гідромашин. Режими роботи гідродинамічної передачі), страница 13

Лобова сила найчастіше визначається експериментально, під’ємна – за формулою

,                       яка виходить із теореми М.Е. Жуковського. Приведена формула дозволяє отримати питому під’ємну силу для лопаті одиничної середньої ширини.

Структуру  потока  рідини  у  робочій  порожнині насоса показано на рис. 5.      

27.

28. Нестійка робота насосів

Виконання умов енергетичного та матеріального балансу (і ), які забеспечують стійку роботу насоса в режимі робочої точки, не завжди є достатнім для забезпечення  стійкої роботи системи “насос-зовнішня мережа”. Стійкістю називають здатність системи повертатись у стан рівноваги після зняття збурення. Умови стійкості можна отримати шляхом аналізу рівняння перехідного процесу, викликаного виведенням системи “насос-мережа” із стану рівноваги

,                                               (1)

де А – коефіцієнт, який характеризує акумулюючу здатність системи.

Розв`язавши рівняння (1) відносно малого відхилення подачі , отримаємо

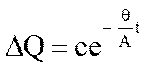                                         ,                                                        (2)

де с – стала інтегрування, а параметр

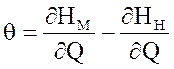.                                                     (3)

Рівновага буде стійкою, коли при , . Оскільки коефіцієнт  - величина позитивна, то при   й , якщо , то умовою стійкості буде виконання нерівності:

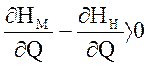.                                                   (4)

Наприклад, для відцентрових насосів, якщо максимальний напір досягається при режимі холостого ходу (Q=0), тобто , то уся характеристика насоса  є областю стійкої роботи (рис.1). Якщо у мережі немає резервуарів, тобто відсутня акумулююча здатність, то уся характеристика насоса є областю стійкої роботи за умови перетинання характеристик  насоса і мережі в одній робочій точці.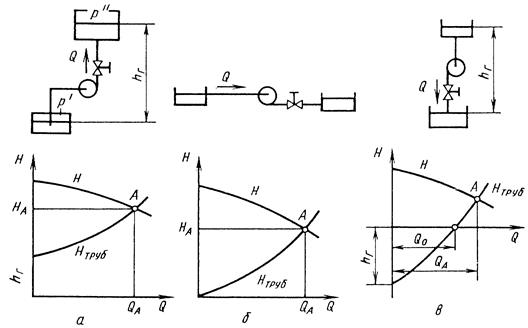

Рис. 1. Визначення режиму роботи насоса на насосну установку при різних значеннях геометричного напору: а - ; б - ; в -

За визначених співвідношень енергетичний баланс між насосом і мережею може мати місце не в одній робочій точці, а в двох (рис.2), до того ж умови роботи у цих точках будуть різними. Режим роботи в точці А  стійкий, тому що тут . У точці Р режим нестійкий: збурення у бік збільшення подачі спричинює перехід режиму роботи в точку А; збурення зворотного знака – перехід режиму в точку С, а потім знову у точку Р.

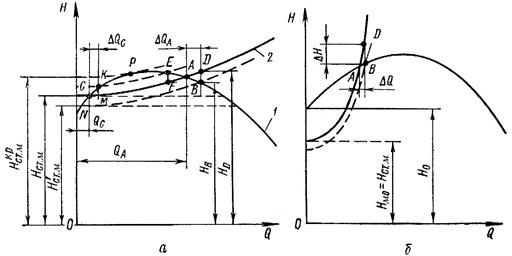Рис. 2. Стійка (а) і нестійка (б) робота насосів

Працювати на висхідній гілці характеристики не рекомендується, тому що у цьому випадку створюються сприятливі умови для нестійкої роботи. Якщо система має характеристику (рис.2,б), за якою: , то робота насоса на висхідній гілці кривої  може бути стійкою (точка А).

За наявності у мережі акумуляторів енергії (парової подушки у котлі, довгих пружних трубопроводів, резервуара із змінним рівнем) амплітуда коливань при порушенні рівноваги може досягати великих значень і робота насоса біля точки максимуму напорної характеристики (точка Р) може бути нестійкою. Виникає помпаж, тобто явище автоколивань у системі “насос-мережа”. При цьому подача різко змінюється від найбільшого значення до нуля, напір коливається у значних межах, спостерігаються удари, шум та струси насоса й трубопроводів.

Розглянемо більш детально роботу системи “насос-зовнішня мережа” (рис.2,а). Нехай при роботі у точці А витрата рідини у системі зростає на  внаслідок короткочасного спаду тиску у напірному резервуарі, тобто короткочасного зменшення значення статичного напору мережі до величини .

У цьому випадку характеристика мережі буде рухатись паралельно собі донизу і робочою точкою системи стане точка В. Після усунення джерела збурення характеристика мережі переміститься угору на колишне місце й витраті рідини  буде відповідати напір  мережі, у той час як при  насос може створити тільки напір . Таким чином, при додатньому значенні  виникає додатна  різниця напорів мережі та насоса

.