скорость, с которой надо ехать,
чтобы приехать вовремя находится в промежутке от 60![]() до
65
до
65![]() .
.
7 класс
Можно ли из чисел 1; -1; 2; -2; … 1998; -1998 выбрать ровно 1999 чисел так, чтобы их сумма равнялась 2000? Обоснуйте свое мнение.
В наборе всего 1998 пар взаимно противоположных чисел.
Принцип получения требуемой суммы: Из предлагаемых чисел составим число 2000, а остальные числа – это пары взаимно противоположных чисел, которые при сложении взаимно уничтожаются.
2000 = 1998 + 2 +(-1), значит количество пар: (1999 – 3) : 2 = 998.
Итак, например, требуемые числа: 1998, 3, -1, 4, -4, …1002, -1002.
Аналогично можно представить другие наборы чисел, например: 1997, 4, -1, 5, -5,…1003, -1003 и так далее.
Если четырехзначное число разделить на 2, или на 9, то в каждом случае получится трехзначное число, записанное тремя одинаковыми цифрами. Найти это число. Придумать аналогичную задачу.
Запишем условия задачи: 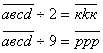
![]()
![]() d – четное
число
d – четное
число
а + в + с + d – делится на 9
По-другому условия задачи можно
переписать следующим образом: 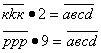
Первое число подберем: возьмем произвольное трехзначное число, записанное тремя одинаковыми цифрами, и умножим его либо на 2, либо на 9:
![]()
Теперь проверим, делится ли полученное числона 9 или является ли четным и получается ли в результате трехзначное число, записанное тремя одинаковыми цифрами:
1+9+9+8=27 – число 1998 делится на 9 (по признаку)
1998 : 9 = 222
Итак, такое число найдено: 1998 (999, 222).
Аналогично можно проверить другие трехзначные числа, записанные двумя одинаковыми цифрами. Такого числа больше нет.
Аналогичная задача может быть построена по нескольким основаниям:
· Подобрать двузначное, пятизначное, шестизначное и т.д. числа.
· Подобрать четырехзначное число, которое если разделить на 3(4,5), или на 8(7,6), то в каждом случае получится трехзначное число, записанное тремя одинаковыми цифрами и т.д.
Полярник едет на собаках к другу. После первого дня пути половина собак убежала, скорость упала вдвое, и полярник опоздал на 2 дня. Если бы он проехал на полной упряжке еще 50 км, и половина собак убежала после этого, то он опоздал бы на 1 день. За сколько дней он планировал доехать до друга?
То, что продолжение движения (еще 50км) позволяет сократить опоздание на 1 день, дает возможность утверждать, что скорость движения на полной упряжке составляет 50 км/день.
До того, как убежали собаки, был пройден 1 день, то есть 50 км.
После того, как собаки убежали, скорость стала составлять 25 км/день.
То условие, что полярник опоздал на 2 дня, говорит о том, что путь пройденный им на не полной упряжке равен 25*4=100 (км).
Значит, Все расстояние: 100+50=150 (км), а это означает, что он планировал добраться за 3 дня.
Учащимся 3-7 классов для выполнения в парах были предложены следующие задачи:
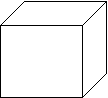
Не нарушая целостности и используя только лист бумаги, линейку и карандаш найти расстояние АВ данной коробки. Разрешается сделать только одно измерение.
Приведем рейтинг решений:
1. Неверным считается решение, в котором не удерживаются начало и конец измерения, подменяются на другие точки.
2. Измерение от точки А до точки В осуществляется по поверхности коробки через точку С.
![]()
 А
А
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.