Работа со сновидениями. Практическое руководство, страница 33

96 : 4 = 24(ч) – количество человек в классе.

Задача №2

Если трехзначное число разделить на 2, или на 9, то в каждом случае получится двузначное число, записанное двумя одинаковыми цифрами. Найти это число. Придумать аналогичную задачу.

Запишем условия задачи: 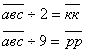 с – четное число

а + в + с – делится на 9

По-другому условия задачи можно переписать следующим образом: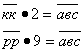

Первое число подберем: возьмем произвольное двузначное число, записанное двумя одинаковыми цифрами, и умножим его либо на 2, либо на 9:

Теперь проверим, делится ли полученное числона 9 или является ли четным и получается ли в результате двузначное число, записанное двумя одинаковыми цифрами:

1+9+8=18 – число 198 делится на 9 (по признаку)

198 : 9 = 22

Итак, такое число найдено: 198 (99, 22).

Аналогично можно проверить другие двузначные числа, записанные двумя одинаковыми цифрами. Такого числа больше нет.

Аналогичная задача может быть построена по нескольким основаниям:

·  Подобрать четырехзначное, пятизначное и т.д. числа.

·  Подобрать трехзначное число, которое если разделить на 3(4,5), или на 8(7,6), то в каждом случае получится двузначное число, записанное двумя одинаковыми цифрами и т.д.

Задача №3

Если ехать из А в В со скоростью 70 км/ч, то приедешь раньше назначенного времени на 40 минут, а если ехать со скоростью 60 км/ч, то опоздаешь на 20 минут. Определить расстояние от А до В и скорость, с которой надо ехать, чтобы приехать вовремя.

Пусть х – точное время,

тогда  х -  - время, которое потратится при езде со скоростью 70,

            х + - время, которое потратится при езде со скоростью 60,

поскольку расстояние одинаковое, можно составить уравнение: .

Решим это уравнение: х=6- это составляет 6ч 40мин.

Найдем расстояние: 60(6 + ) =420(км).

Найдем скорость: 420 : 6 = 63().

Можно решить задачу, составив систему уравнений.

Пусть х – расстояние между пунктами А и В, у – точное время,

Тогда  - время, которое потратится при езде со скоростью 70,

             - время, которое потратится при езде со скоростью 60.

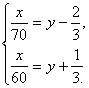  Решив систему, получим  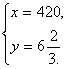Найдем скорость 420 : =63().

Можно решить задачу, следующими рассуждениями.

При скорости в 70 происходит сокращение точного времени, а при скорости в 60 - опоздание,

 значит скорость, с которой надо ехать, чтобы приехать вовремя находится в промежутке от 60до 70, более того, из разницы опоздания и обгона следует, что