Так
как ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() .
.
Площади поперечных сечений стержня:
![]() ,
, ![]() ,
, ![]() .
.
Длины участков стержня:
![]() ,
, ![]() ,
, ![]() ,
, ![]()
Подставив значения величин, получим
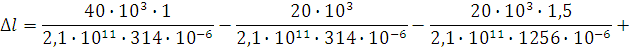
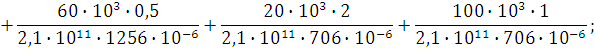
![]()
![]() или
или ![]()
Задача 1.5.
Стальной
стержень круглого поперечного сечения находится под действием продольной силы ![]() и
равномерно распределенной нагрузки
и
равномерно распределенной нагрузки ![]() (рис.
1.8). Требуется построить эпюру продольных усилий
(рис.
1.8). Требуется построить эпюру продольных усилий ![]() ,
подобрать сечение из условия прочности
,
подобрать сечение из условия прочности ![]() и
построить эпюру перемещений
и
построить эпюру перемещений ![]() .
.
Решение
1.
В данной задаче необходимо разбить стержень на два участка (рис. 1.8). Начиная
со свободного конца стержня, мысленно разрезаем каждый участок в произвольном
сечении с координатой ![]() и
записываем выражение для продольной силы (при этом сжимающая сила считается отрицательной,
а растягивающая – положительной).
и
записываем выражение для продольной силы (при этом сжимающая сила считается отрицательной,
а растягивающая – положительной).
I
участок: ![]()
![]()
![]()
![]()
II
участок: ![]()
![]()
![]()
2. По найденным значениям строим эпюру продольных
усилий ![]() .
.
3. Опасным является сечение, в котором действует
максимальная внутренняя сила ![]() . Из
условия прочности при растяжении-сжатии находим требуемую площадь поперечного
сечения стержня:
. Из
условия прочности при растяжении-сжатии находим требуемую площадь поперечного
сечения стержня:
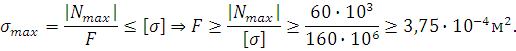
Тогда для круглого поперечного сечения диаметр будет равен:
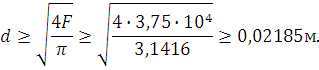
Принимаем ![]()
Фактическая площадь поперечного сечения ![]() .
.
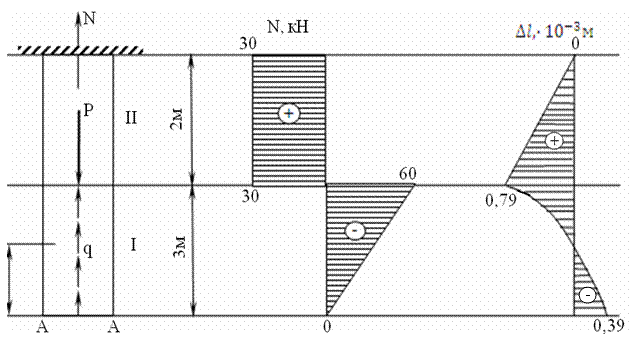
Рис. 1.8
4. Используя формулу для расчета деформаций стержня при растяжении-сжатии, рассчитываем удлинения отдельных участков. При этом необходимо помнить, что на участке с распределенной нагрузкой зависимость удлинения от координаты сечения нелинейная, и графиком будет являться парабола.
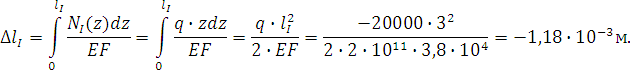
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.