К практическим занятиям, самостоятельному изучению и выполнению контрольных и расчетно-графических работ по темам: «Растяжение и сжатие», «Геометрические характеристики плоских сечений», «Кручение», «Прямой изгиб», страница 3

, или .

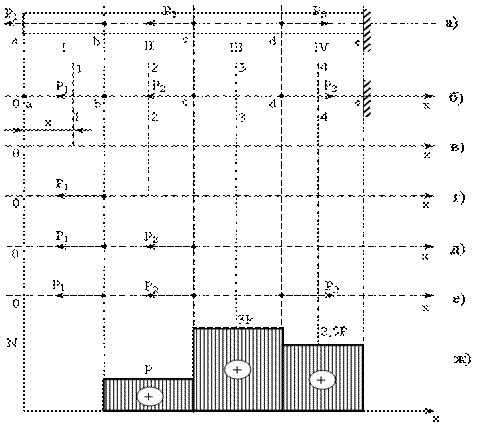
Рис. 1.1

         Аналогично мысленно проведем сечение 2-2 в пределах участка II (рис. 1.1г). Тогда, из условия равновесия , следует, что: . Отсюда .

         Тогда для третьего участка, проводя сечение 3-3 (рис. 1.1д), можно записать

, или .

         Для четвертого участка, проводя сечение 4-4 (рис. 1.1е), запишем

, или .

         Пусть,

тогда .

         Построим эпюру продольных сил для данного бруса (рис. 1.1ж).

         Из эпюры видно, что сила реакции опоры составляет .

         Пример 1.2.  Рассмотрим случай, когда в поперечном сечении балки приложена распределенная сила в направлении оси балки (рис. 1.2а). На практике такой распределенной силой может быть сила тяжести бруса (рис. 1.2 а).

Выделим два участка по длине бруса. Начало координат поместим на свободном конце бруса и ось х направим по длине бруса. Проведем сечение 1-1 на расстоянии х от начала координат. Тогда продольная сила на участке I при  будет равна .

         , .

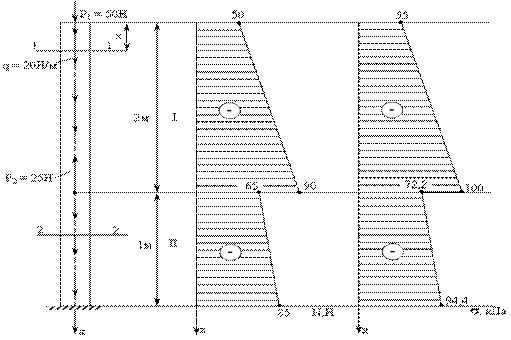
                  а)                                            б)                                  в)

Рис. 1.2

         Проведем сечение 2-2 на втором участке, т.е. .

,

; .

         Построим эпюру продольных сил (рис. 1.2а).

         Определим продольные напряжения в брусе, при условии, что площадь поперечного сечения бруса постоянная по длине и равна . Тогда напряжение на участках будет равно

; ,

.

,

;

.

.

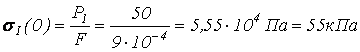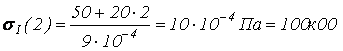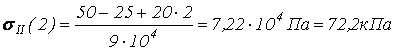
         Построим эпюру нормальных напряжений (рис. 1.2в).

         Вследствие возникновения продольных сил в образце происходит изменение длины образца.

         Абсолютное удлинение бруса выражается формулой:

,                                                  (1.1)

где     – величина продольной силы, действующей в брусе;