К практическим занятиям, самостоятельному изучению и выполнению контрольных и расчетно-графических работ по темам: «Растяжение и сжатие», «Геометрические характеристики плоских сечений», «Кручение», «Прямой изгиб», страница 22

где     – жесткость сечения при кручении;

          – модуль сдвига;

          – полярный момент инерции сечения.

         Для круга

.

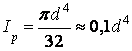         Для кольца

.

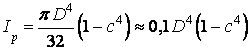         При  и  угол закручивания участка длиной  определяется по формуле

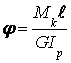, рад.

         Условие жесткости при кручении имеет вид

, град.,

или

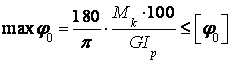, град.

3.2. Расчеты на прочность и жесткость при кручении бруса круглого поперечного сечения. Статически определимые задачи.

         Рассмотрим решение некоторых типов задач по определению диаметра вала.

Задача 3.1.

         Для двух брусьев (рис. 3.1а, 3.2а), работающих на кручение, построить эпюры крутящего момента .

         Дано: , ,

Решение

         Определение крутящего момента в сечениях бруса начинаем от его свободного левого конца, тогда определение его реакции защемления – пары сил с моментом , необязательно. Делим брус на силовые участки. По условию задачи брус содержит четыре силовых участка.

I участок

Проведем на участке поперечное сечение 1-1, мысленно отбросим правую часть бруса, а к оставшейся части приложим крутящий момент  таким образом, чтобы при взгляде на сечение со стороны внешней нормали он был направлен против часовой стрелки. Рассмотрим равновесие оставшейся части:

;

Первый брус

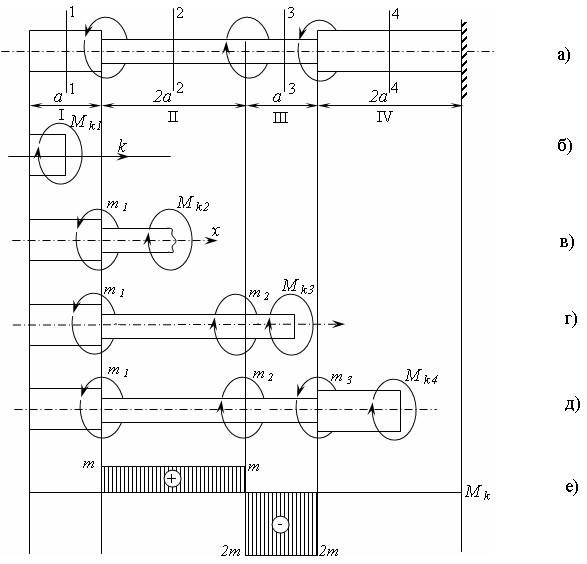
Рис. 3.1

         II участок

;

;

.

         III участок

;

;

.

         IV участок

;

;

.

         Отсутствие крутящего момента в сечении заделки указывает на то, что ее реакция .

Второй брус

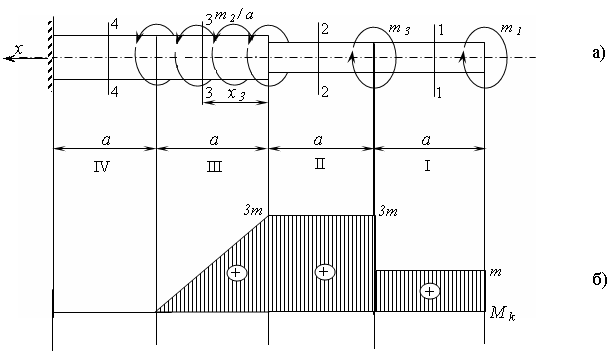
Рис. 3.2

Решение

         Определение крутящего момента в сечениях бруса начинаем от его правого свободного конца.

         I участок

;

;