К практическим занятиям, самостоятельному изучению и выполнению контрольных и расчетно-графических работ по темам: «Растяжение и сжатие», «Геометрические характеристики плоских сечений», «Кручение», «Прямой изгиб», страница 19

см; см;

см; см.

         3) Используя формулы перехода к параллельным осям, рассчитываем осевые (экваториальные) и центробежные моменты инерции всего сечения относительно осей :

         4) Положение главных центральных осей определяется углом поворота :

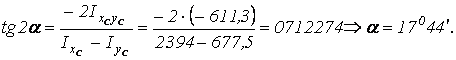
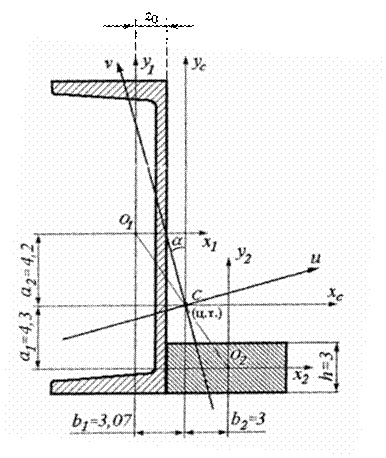
Рис. 2.5

         Проводим через центр тяжести под углом  главные центральные оси u и v. Так как , то угол откладывается против часовой стрелки.

         5) Рассчитываем главные (экстремальные) моменты инерции. Из рисунка видно, что , .

         Проверка:

Задача 2.4.

         Дано: рис. 2.6, швеллер №14, равнобокий уголок 100 х 100 х 10.

Решение

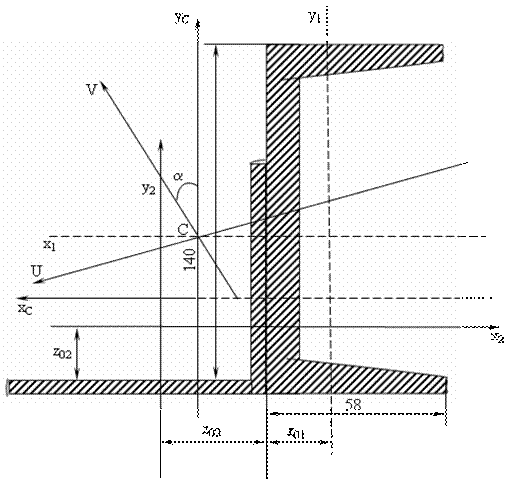
Рис. 2.6.

         1. Для швеллера №14:

         см, см⁴, см³, см, см⁴, см⁴, см³, см, см².

         2. Для равнобокого уголка 100 х 100 х 10:

         см², см, см⁴, см, см⁴, .

         3. Выберем вспомогательные оси  и определяем положение центра тяжести всего сечения:

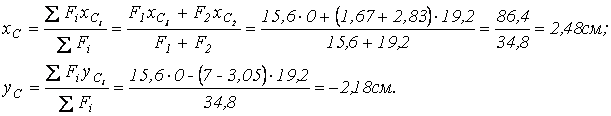
         Центр тяжести фигуры С (2,48см, -2,18см).

Через точку С проведем оси параллельные  и , центральные оси  и .

         Находим центры тяжести отдельных фигур относительно осей  и .

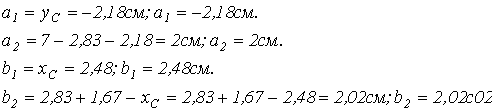
         4. Рассчитаем осевые и центробежные моменты инерции всего сечения относительно осей :