К практическим занятиям, самостоятельному изучению и выполнению контрольных и расчетно-графических работ по темам: «Растяжение и сжатие», «Геометрические характеристики плоских сечений», «Кручение», «Прямой изгиб», страница 28

         Условие перемещений

.

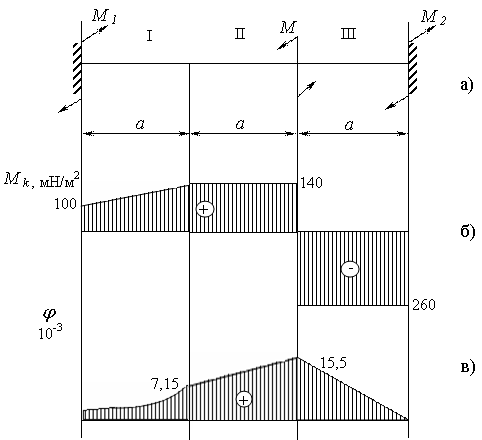
Рис. 3.9

         Так как жесткость сечения стержня постоянная, то последнее уравнение перепишется в следующем виде

,

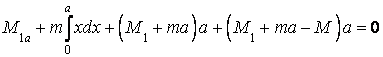отсюда

.

Нм.

         Подставляя  в уравнение статики, находим

Нм.

         Строим эпюру крутящего момента (рис. 3.9б).

         По расчетной формуле

.

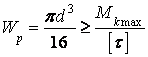         Отсюда

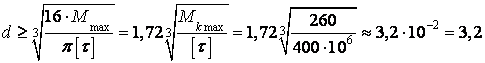см;

см.

         Находим углы закручивания.

;

;

;

;

;

;

;

.

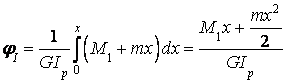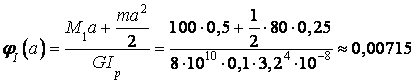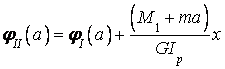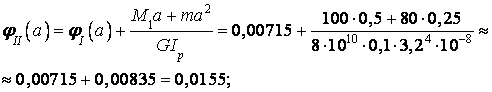
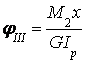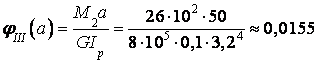На рис. 3.9в представлена эпюра углов закручивания стержня.

Задача 3.9.

         Стальной брус защемлен по концам (рис. 3.10а); нагружение парами сил  и ; имеет поперечные сечения: прямоугольное, круглое, круглое кольцевое. Требуется подобрать размеры поперечного сечения бруса, принимая значения момента пары сил Нм. Применить величину допускаемого касательного напряжения мПа.

         Дано: , , , , , .

Рис. 3.10

         1. Определяем степень статической неопределимости. Отбрасываем заделки и заменяем их реакциями – парами сил с моментом  и , направление которых выбираем произвольно. Составим уравнение равновесия бруса при кручении (рис. 3.10б).

;

,                                        (1)

         Уравнение содержит два неизвестных – задача один раз статически неопределима.

         2. Раскрываем статическую неопределимость, исходя их того, что суммарная деформация от действия моментов ,  и  в сечении А равна нулю

.

         Согласно принципу независимости действия сил

,                                     (2)