К практическим занятиям, самостоятельному изучению и выполнению контрольных и расчетно-графических работ по темам: «Растяжение и сжатие», «Геометрические характеристики плоских сечений», «Кручение», «Прямой изгиб», страница 42

, где ;

при              ;

при               Нм.

         Построим эпюры  и .

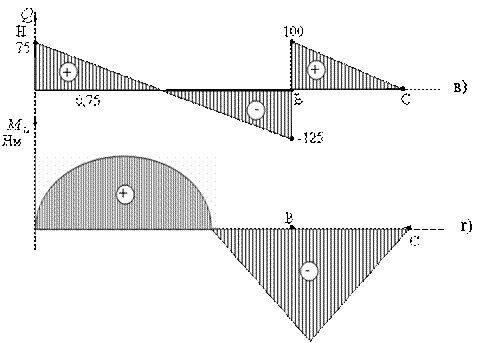
Рис. 4.16.

Задача 4.10.

Считая балку двутавровой, определить номер сечения из расчета на прочность, если допускаемое напряжение при изгибе Мпа, Н, Н/м, м.

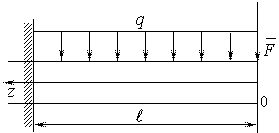
Рис. 4.18 а

Решение

         Начало координат выберем на свободном конце балки. Если балка имеет один участок, то изгибающий момент будет

, где .

         На границах:

при    ;

при Нм.

         Максимальное значение изгибающий момент имеет в защемленном конце

Нм.

         Так как ,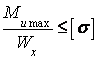

где     – момент сопротивления изгибу.

         Отсюда см³.

         Отсюда следует (по таблице), что выбираем двутавровое сечение №12, для которого см³.

         Эпюра:

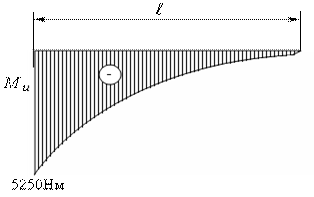
Рис. 4.18 б.

         4.3. Расчеты на прочность по нормальным напряжениям

         При прямом чистом изгибе балки в поперечных сечениях ее возникают нормальные напряжения, величина которых зависит от значения изгибающего момента в соответствующем сечении. При прямом поперечном изгибе, кроме того, возникают касательные напряжения, связанные с поперечной силой.

         Нормальное напряжение в любой точке поперечного сечения определяется по формуле

,

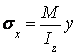где     – изгибающий момент в данном сечении;

          – момент инерции сечения относительно нейтральной оси;

 – расстояние от точки, где определяется напряжение, до нейтральной оси (рис. 4.19. а,б).

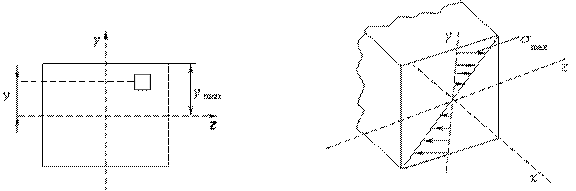
                            а)                                                               б)

Рис. 4.19.

         Максимальные нормальные напряжения возникают в точках наиболее удаленных от нейтральной оси

,

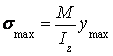или, вводя обозначение 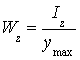, получаем

.

         Условие прочности при прямом изгибе