К практическим занятиям, самостоятельному изучению и выполнению контрольных и расчетно-графических работ по темам: «Растяжение и сжатие», «Геометрические характеристики плоских сечений», «Кручение», «Прямой изгиб», страница 4

          – длина бруса;

          – модуль Юнга;

          – площадь поперечного сечения бруса.

         Произведение  называется жесткостью поперечного сечения бруса.

         Удлинение бруса от равномерно распределенной нагрузки по длине бруса выражается формулой:

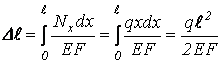,                              (1.2)

где     – равномерно распределенная нагрузка на длине  бруса.

         Удлинение бруса, связанное с силой тяжести, определяется по формуле:

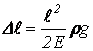,                                              (1.3)

где     – плотность материала бруса;

                   – ускорение свободного падения.

                  При переменных  и  (или одной из этих величин):

.

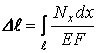                  В общем случае, когда законы  и  для отдельных участков бруса различны:

.

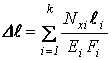                  Условие прочности: ,

где     – допускаемое напряжение.

                  Определение требуемой площади поперечного сечения производится по формуле:

.

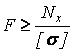                  Определение величины допускаемой продольной силы:

.

                  Рассмотрим примеры определения поперечных сечений бруса.

                  Пример 1.3. Определить общее изменение длины бруса рассмотренного в примере 1.

На рис. 1.3. представлен брус, к которому приложены силы , , площадь поперечного сечения бруса  см², модуль упругости  (сталь Ст3СП), .

Рис. 1.3

                  Разобьем длину бруса на участки (аналогично как в примере 1). Было вычислено, что , , , . Тогда удлинение бруса на первом участке согласно формуле (1.1) будет . На втором участке удлинение бруса равно:

; .

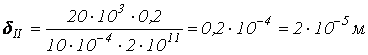                  На третьем участке удлинение бруса равно:

; .

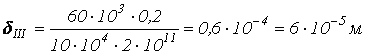                  На четвертом участке удлинение бруса равно: