К практическим занятиям, самостоятельному изучению и выполнению контрольных и расчетно-графических работ по темам: «Растяжение и сжатие», «Геометрические характеристики плоских сечений», «Кручение», «Прямой изгиб», страница 18

– для швеллера:

– для уголка:

– для всего сечения:

         Осевые моменты инерции относительно оси :

– для швеллера:

– для уголка:

– для всего сечения:

         Вычислим центробежный момент инерции относительно осей  и :

– для швеллера:

– для уголка:

– для всего сечения:

.

         Определим положение главных центральных осей инерции сечения.

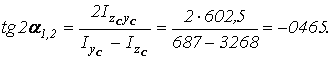
         Главные центральные оси  и  показаны на рис. 2.3. Вычисляем главные центральные моменты инерции.

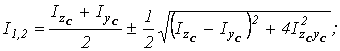
Задача 2.3.

         Для сечения, состоящего из швеллера №20 и прямоугольной полосы  мм (рис. 2.5) необходимо определить положение центра тяжести, найти осевые и центробежный моменты инерции относительно осей, проходящих через центр тяжести всего сечения, определить направление главных центральных осей (uи v) и найти моменты инерции относительно этих осей.

Решение

1) Из сортамента выписываем необходимые данные для швеллера (собственные центральные оси швеллера обозначим ):

см²,

 см²;  см².

 см.

         Рассчитываем площадь поперечного сечения и моменты инерции полосы относительно собственных главных центральных осей :

 см².

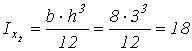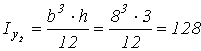см⁴; см⁴.

         2) В качестве вспомогательных осей выбираем оси  и определяем положение центра тяжести всего сечения:

см;

см.

         Через точку С с координатами () проводим параллельно осям  центральные оси  и . В системе координат  по чертежу находим координаты центров тяжести отдельных фигур (О₁, О₂ на рис. 2.5).