К практическим занятиям, самостоятельному изучению и выполнению контрольных и расчетно-графических работ по темам: «Растяжение и сжатие», «Геометрические характеристики плоских сечений», «Кручение», «Прямой изгиб», страница 21

Для уголка:

Для всего сечения:

         Осевые моменты инерции относительно оси :

         Для швеллера:

         Для уголка:

         Для всего сечения: см⁴;

см⁴.

         Вычислим центробежный момент инерции относительно осей  и :

         Для швеллера:

         Для уголка:

         Для всего сечения:

         3. Определить направления главных центральных осей  и .

         4. Найти величины моментов инерции относительно главных центральных осей:

        

        

        

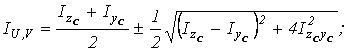
         Проверка:

3. Кручение

         3.1. Основные понятия и зависимости

         При работе бруса на кручение в его поперечных сечениях возникает только один внутренний силовой фактор – крутящий момент .

         В любом поперечном сечении бруса крутящий момент численно равен алгебраической сумме внешних скручивающих моментов приложенных по одну сторону от рассматриваемого сечения.

         Условие прочности при кручении бруса круглого (сплошного или кольцевого) поперечного сечения имеет вид

,

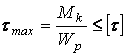где     – наибольшее касательное напряжение, возникающее в опасном сечении бруса;

          – крутящий момент в опасном сечении бруса;

          – допускаемое напряжение (касательное) при кручении;

          – полярный момент сопротивления сечения;

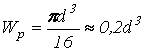          – для круглого сплошного сечения;

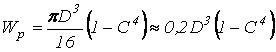          – для кольцевого сечения;

          – диаметр сплошного сечения;

          и  – соответственно наружный и внутренний диаметры кольца.

         Угол поворота одного сечения относительно другого называется углом закручивания участка бруса между этими сечениями.

         Угол закручивания бруса определяется по формуле

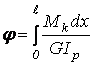, радиан,