К практическим занятиям, самостоятельному изучению и выполнению контрольных и расчетно-графических работ по темам: «Растяжение и сжатие», «Геометрические характеристики плоских сечений», «Кручение», «Прямой изгиб», страница 37

         2. Строим эпюры поперечных сил и изгибающих моментов по характерным сечениям балки.

         I участок:

         Так как на участке отсутствует распределенная нагрузка, то эпюра поперечной силы  ограничена прямой, параллельной осевой линии, а эпюра изгибающего момента  – прямой, наклонной к осевой линии.

.

; .

         II участок:

         Участок нагружен равномерно распределенной нагрузкой, интенсивностью . Эпюра  ограничена прямой, наклонной к осевой линии; эпюра  – квадратной параболой.

         В точке С эпюра  имеет скачок на величину и по направлению силы : .

         В точке В эпюра  имеет скачок на величину и по направлению силы .

         На участке эпюра  пересекает осевую линию в точке с абсциссой . В этой точке эпюра  имеет максимум. Запишем выражение для поперечной силы  на II участке и направляем его к нулю

,

откуда

.

.

.

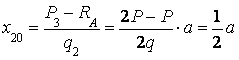         III участок:

         Поперечная сила  для всех сечений участка. Эпюра  ограничена прямой, параллельной осевой линии . В точке D эпюра  имеет скачок на величину и по направлению момента .

Задача 4.2.

         Построить эпюры изгибающих моментов и поперечных сил для нагруженной балки, изображенной на рис. 4.10а.

         Дано: , , . Учесть, что .

Рис. 4.10а

Решение

         Определим силы реакции опор в точках А и В.

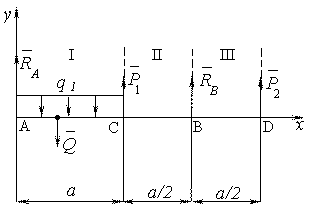
Рис. 4.10б

         Составим условие равновесия балки

; ; ; .

.

.

.

.