К практическим занятиям, самостоятельному изучению и выполнению контрольных и расчетно-графических работ по темам: «Растяжение и сжатие», «Геометрические характеристики плоских сечений», «Кручение», «Прямой изгиб», страница 16

         а) Сумма осевых моментов инерции сечения относительно двух координатных осей равна полярному моменту инерции относительно начала координат

.

         б) Момент инерции (сложного) составного сечения равен алгебраической сумме моментов инерции составляющих сечение частей.

         в) Осевые и полярный моменты инерции сечения – величины существенно положительные; центробежный момент инерции может быть положительным, отрицательным и, для неполярных осей, равным нулю.

         г) Если сечение имеет ось симметрии, то центробежный момент инерции относительно этой оси и ей перпендикулярной равен нулю.

Параллельный перенос осей

         Момент инерции сечения относительно любой оси, проведенной параллельно центральной, равен моменту инерции относительно этой центральной оси плюс произведение площади сечения на квадрат расстояния между осями (рис. 2.2.)

.

Рис. 2.2

         Аналогично .

         Величина a и b должны быть подставлены со своими знаками, определяемыми из условия, что они представляют собой координаты новой системы осей в старой системе координат.

Поворот координатных осей

Если известны моменты инерции сечения , ,  относительно осей  и , то моменты инерции относительно осей  и , повернутых на угол  по отношению к исходным осям определяются по формулам

Главные оси инерции. Главные моменты инерции

         Главными осями инерции называют две взаимноперпендикулярные оси, относительно которых центробежный момент инерции равен нулю, а осевые моменты приобретают экстремальные значения (max и min).

         Если главные оси проходят через центр тяжести фигуры, то они называются главными центральными осями инерции.

         Главные моменты инерции вычисляют по формуле

.

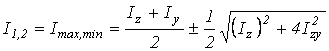         Положение главных осей инерции находят из следующих зависимостей

         Можно также пользоваться формулой

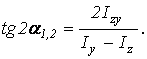
         Углы  и  отсчитывают от положительного направления оси z, причем при  угол откладывают против часовой стрелки, и почасовой стрелке при .

         Выполняется условие

         В таблице 2.1. приведены значения моментов инерции некоторых часто встречающихся сечений.

Таблица 2.1.

Значения моментов инерции наиболее употребляемых сечений относительно центральных осей

Вид сечения (фигуры) и наименование				Моменты инерции
1				2			3
Прямоугольник
Продолжение таблицы 2.1.
1	2		3		4
Треугольник					–
Круг
Полукруг
Кольцо
Эллипс