Пример 1.4. Для бруса жестко закрепленного обоими концами (рис. 1.9а) определить реакции заделки, построить эпюры продольных сил и нормальных напряжений.
Под
действием внешних сил возникают силы реакции опор 
и 
.
Уравнение равновесия имеет вид: 
.
Так как брус с двух сторон защемлен, то перемещения
сечений А и В равны нулю. Отбросим, например, нижнее закрепление и заменим его
действие неизвестной силой реакции (рис.
1.9б). Определим перемещение сечения В от известной внешней силы Р:
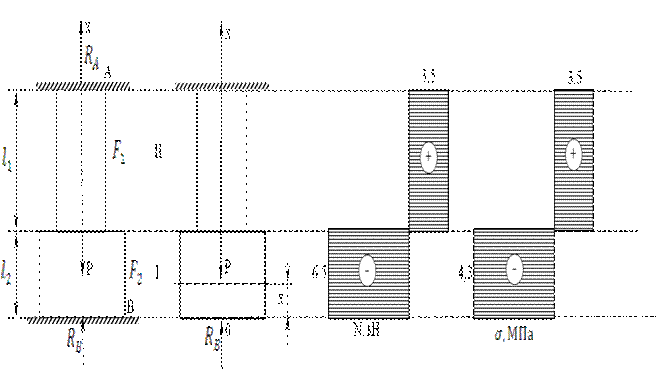
а) б) в) г)
Рис. 1.9
Перемещение сечения В от неизвестной силы :
Общее перемещение сечения В от совместного действия
сил Р и равно:
Но переменное сечение В должно быть равно нулю:
Тогда 
отсюда:
или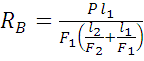 
.
; 
; 
;
.
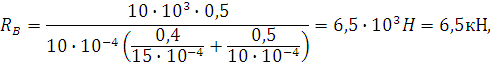
Из условия равновесия бруса: 
,
.
Определим продольные силы и напряжения по длине бруса.
Поместим начало координат на свободном конце (сечение В) и направим ось х по длине бруса.
Разделим длину бруса на два участка. Первый участок нумеруем со свободного конца.
По методу сечений определим для первого участка:
,
.
Для второго участка:
,
.
На первом участке напряжение:
На втором участке напряжение:
На рис. 1.9в, г представлены эпюры продольных сил и нормальных напряжений.
Рассмотрим решения задач на раскрытие статической неопределимости для стержневых систем. Балку считать абсолютно твердым телом, учитывать только деформируемость стержней.
Задача 1.4.
Дано: определит абсолютное удлинение стержня по условиям задачи 1.2.
Решение
Абсолютное удлинение стержня равно алгебраической сумме абсолютных удлинений его участков:
,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.