Ответы на экзаменационные вопросы № 1-40 по дисциплине «Радиосистемы управления» (Назначение и состав систем радиоуправления. Управление бортовой аппаратурой с командного пункта), страница 5

     Если частота ω₀ собственных угловых колебаний корпуса ЛА  относительно вектора скорости   значительно выше граничной частоты общего контура управления ω_к , то колебательный множитель в знаменателе может быть опущен. Передаточную функцию (1.6) можно заменить ее эквивалентом

                                                                             (1.7)

или

                                                                          (1.8).

Необходимым условием замены (1.6) одним из эквивалентов (1.7) или (1.8) является соблюдение равенства  установившихся значений ошибок, т.е. сохранение порядка астатизма системы. Второе, желательное  условие – соразмерность собственного периода колебаний и времени затухания переходного процесса в реальной и эквивалентной системах. Ошибка управления в системе наведения (основное уравнение системы наведения как   системы автоматического регулирования)

                                                                                              (1.9)

где первое слагаемое – текущая координата кинематической траектории, второе

                -  текущая координата динамической или фактической траектории.

В процессе движения объекта его кинематическая траектория изменяется и  должна в каждый новый момент времени вычисляться от соответствующей точки на   динамической траектории. Однако, если управление по кинематической траектории  происходит достаточно точно, эту особенность можно не учитывать и при расчетах  ошибок пользоваться выражением (1.9) как равенством.

                        Функцию управления  в  угловых или линейных координатах, в большинстве случаев описывают рядом по степеням (типовое воздействие в виде полиномиальной функции)

                                  = A₀+A₁t+A₂t²+……+A_ntⁿ…                 (1.10).

             A₀ – начальное значение задающего воздействия; A₁ ()-начальная скорость изменения  задающего воздействия; A₂- начальное ускорение, с которым изменяется задающее воздействие.       

             Тогда ошибка наведения

                                                                     (1.11)

               может быть пре6дставлена в виде ряда

                                 (1.12)

               где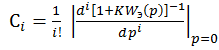- коэффициенты ошибок, - передаточная функция   для ошибки по задающему воздействию.Для систем с астатизмом первого порядка С₀=0 и ошибка по положению равна  нулю. Для систем с астатизмом второго порядка С₀=С₁=0, т.е. отсутствуют ошибки по   положению и скорости.

    Число членов ряда (1.12) при выбранной управляющей функции для заданной

 траектории наведения и предполагаемого маневра цели определяется из условия

                    (1.13)

где t_max- предварительно вычисленное максимальное значение времени движения ЛА до цели по кинематической траектории.

    При известных t_max и n ошибка наведения определяется по формуле

        (1.14)

    Динамические ошибки тем больше, чем больше инерционность или постоянная  

времени системы управления.                  

            Кроме динамической ошибки  в процессе наведения могут образовываться ошибки за счет воздействия ветра или воздушных течений. Когда скорость и направление ветра  известны и могут быть приняты постоянными, ошибки в одной иплоскости движения рассчитываются по известным методам учета возмущающих воздействий в виде

                                                                 (1.15)

            где  - функция передачи части общего контура системы управления с функцией

            передачи  от точки приложения вектора  до выхода из системы.

Если к входу системы приложены два воздействия: задающее и возмущающее v(t), причем взаимная корреляция между ними отсутствует, то средний

            квадрат результирующей ошибки Δφ определяется суммой двух составляющих ошибки   по задающему воздействию и помехе

                                                            (1.16)      

                                                                          v(t)