 |
δ
Рисунок 2.22 - Структурная схема рулевого тракта
Рулевые машины приводятся в движение выходным напряжением усилителя сигнала рассогласования, т.е. разностью между входным напряжением и напряжением обратной связи (ОС). Для усиления низкочастотного сигнала ошибки используются магнитные или полупроводниковые усилители, обеспечивающие требуемую выходную мощность.
Угол поворота руля δ измеряется потенциометричеким датчиком, напряжение которого используется для жесткой ОС. Корпус датчика крепится неподвижно относительно корпуса ракеты, а движок жестко связывается с валом руля. При повороте руля движок поворачивается и снимаемое напряжение оказывается пропорциональным углу поворота.
Скорость измерения угла поворота руля измеряется тахогенератором, т.е. генератором переменного или постоянного тока, вырабатывающим напряжение, пропорциональное скорости вращения ротора. Корпус генератора неподвижен, а вал ротора связывается с помощью зубчатой передачи с валом руля. Сигнал тахогенератора используется для демпфирования привода (гибкая ОС).
Передаточную функцию прямой цепи рулевого тракта, состоящей из электрической рулевой машины, нагруженной рулем, и усилителя, можно записать
(2.6)
где 
- постоянная времени рулевой
машины, а 
- коэффициент передачи, имеющий
размерность град/В·с из-за наличия интегральной связи между входным
напряжением и выходным углом поворота.
Введение ОС по углу и скорости изменения угла дает нам передаточную функцию цепи ОС в виде:
(2.7)
и 
;
- напряжение обратной связи на
входе усилителя; 
- добротность привода управления
рулем.
Передаточная функция замкнутого контура рулевого тракта оказывается равной
, (2.8)
где
; 
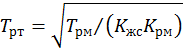- соответственно коэффициент усиления, постоянная времени и коэффициент затухания.
Коэффициент затухания является функцией добротности привода, которая может быть изменена подбором масштаба напряжений гибкой и жесткой ОС, существенно влияя на характер переходного процесса.
15. В отсутствие автопилота (АП) движение описывается системой нелинейных дифференциальных уравнений, которые в векторной (сокращенной) форме имеют вид
, 
Однако сложное движение ЛА можно представить в виде ряда простых: плоского продольного движения (полет на заданной высоте, набор высоты, снижение), бокового движения (чистое рыскание, плоский и координированный развороты), - что значительно упрощает математическое описание движения и процесса управления.
1. Уравнения движения ЛА в связанной системе координат при плоском продольном движении в отсутствие возмущающих сил имеют вид
,
,
, (2.16)
,
,
Из этих соотношений можно, опуская промежуточные выкладки [8], выразить функциональной зависимостью между углом тангажа и отклонением руля высоты .
,
Функциональная
связь между углом наклона траектории Δθ и отклонением руля высоты
в записывается в виде
. (2.18)
Здесь
- угол наклона траектории.
В
соответствии с функциями передачи данная структурная схема содержит
колебательное звено и два идеальных интегратора. Управление высотой полета по
данной схеме при пропорциональном отклонении рулей высоты 
является неустойчивым, так как в контур управления
входят два идеальных интегратора. Устойчивость может быть достигнута, если в
закон управления рулями ввести производную от высоты или фазовое опережение,
т.е. 
, или, охватив жесткой обратной связью один из
интеграторов, понизить порядок астатизма контура управления.
2. В случае плоского бокового движения функции передачи, описывающие связь курсового ψ и путевого Φ углов с отклонениями руля направления δн , имеют вид аналогичный уже приведенным выражениям,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.