/s(t)« B'm - закон Бейли,
/,((). (1 + btv*)exp(*t) - закон Андраде,
/а (t) - S a,-1 ' - закон Грэхема и Уоллеса.
 i
i
В соответствии с законом Аррениуса зависимость от температуры имеет вид
/,(Т)-4ехр(-ДИ/кТ).
Здесь Дй - энергия активации, к — постоянная Больцмана, Т — абсолютная температура.
Наиболее часто используется на практике зависимость ес(а ,t. Т), объединяющая простейшие из приведенных выше выражений: бс-Сехр(-ДЯ/кТ)*то-п,
откуда при постоянной температуре имеем
«с - Btman. (2Л)
Приведенные формулы пригодны, разумеется, только для случая постоянных напряжений и представляют собой попытку математической формализации первой и второй стадий ползучести. При переменных напряжениях будем рассматривать зависимости скоростного типа: например, из соотношения (2,1) вытекает при о- - const следующая зависимость:
at
(2.2)
которую можно, используя одновременно соотношения (2.1) и (2.2), преобразовать к форме, не содержащей времени £•:
^.тД«Л»сг-'»Л<.1 -""*. (2-3)
Выбор зависимости скоростного типа является попыткой математического моделирования первой стадии ползучести, когда скорость ползучести убывает — этот процесс часто называют упрочнением. Обычно говорят,
28
Глава 2.Феноменологическое описание ползучести
Эксперимент при 216°С &
что соотношение (2.2) отражает временное упрочнение, поскольку фаза упрочнения здесь моделируется с использованием в качестве параметра временной переменной. По аналогичной причине соотношение (2.3) называют моделью деформационного упрочнения1) „ Разумеется, понятия временного и Деформационного упрочнений могут быть введены и для функций, отличных от простейшей зависимости (2.1).
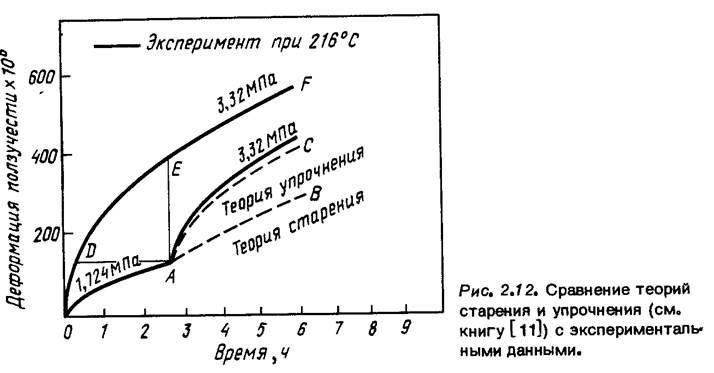
Очевидно, обе модели при постоянном напряжении приводят к одному и тому же результату. Однако если предположить, что они применимы и в условиях, когда напряжение меняется произвольным образом, то мы найдем, что эти модели дают различные результаты. Сравнение результатов для случая ступенчатого нагружения дано на рис. 2.12. Из уравнения (2.2) следует, что скорость деформации в любой момент времени зависит от промежутка времени от начала нагружения, в то время как из (2.3) вытекает, что эта скорость зависит от накопленной деформации ползучести. Различие проще понять, если обратиться к кривым на рис. 2.12.
Кривая ОАС — экспериментальная и соответствует ступенчатому нагруже-нию; кривая OF соответствует эксперименту на ползучесть при постоянной нагрузке, равной нагрузке в конце второй ступени нагружения. Кривая АВ, рассчитанная по модели временного упрочнения, получается смещением куска EFкривой OFвертикально вниз до точки А. Кривая ползучести АС, предсказываемая моделью деформационного упрочнения, получается с использованием перемещения куска DFкривой OF по горизонтали до точки А, Очевидно, худшие результаты дает модель временного упрочнения. Однако в
*'в отечественной литературе модель временного упрочнения называют теорией старения, модель деформационного упрочнения — теорией упрочнения. — Прим. перев.
2 3. Простейшие одномерные определяющие уравнения
29
случае непрерывного изменения нагрузки различие в результатах уменьшается, в то же время соотношение (2.2) проще для применения на практике.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.