Методы ана­лиза напряжений в конструкциях с учетом деформаций ползучести, страница 14

Численные результаты особого интереса не представляют, поскольку и материал, и история нагружения выбраны достаточно произвольно. Однако некоторые качественные особенности поведения конструкции все-таки можно выявить. В частности, из кривых на рис. 7.13 видно, что процесс деформиро­вания имеет четыре различных этапа. За начальной упругой деформацией сле­дует этап быстрого роста деформаций "ползучести", накапливаемых в тече­ние очень короткого промежутка времени — на самом деле это обычная плас­тическая деформация. Далее следует начальная стадия ползучести и, наконец, этап установившейся ползучести, который прерывается скачкообразным рос­том нагрузки.

7.6. ЧИСЛЕННОЕ РЕШЕНИЕ КРАЕВЫХ ЗАДАЧ ТЕОРИИ НЕУСТАНОВИВШЕЙСЯ ПОЛЗУЧЕСТИ МЕТОДОМ КОНЕЧНЫХ ЭЛЕМЕНТОВ

В этом разделе мы кратко обсудим практическую реализацию описанных выше алгоритмов численного интегрирования в методе конечных элементов. Остановимся лишь на основных особенностях метода. Используемые обозна­чения в основном стандартные: симметричные тензоры напряжений и дефор­маций представляются шестикомпонентными векторами а и с, поле вектора перемещений — трехкомпонентным вектором и. Связь деформаций с переме­щениями определяется линейным дифференциальным оператором • -[I]»,

(7.29)

где

[Il-v.

" д	0	П	0      д	а  ~
а*,			Эх	д*2
о	д	о	3о	д
	дхг		дх3	дх,
о	0	д	д     д	о
		(>Х	дх     f)x
_		3	2           1	__

Полная деформация представляется суммой упругой деформации е_£ и дефор-

мации ползучести е   :

•  = ^ЕЕ "С ,<⁷-³⁰>

причем упругая деформация линейно связана с напряжением:

« = [D]«_E.                                                                                                  (7.31)

где [D] — матрица упругих модулей размерности 6х 6. Для простоты темпера­турными деформациями будем пренебрегать.

7.6. Метод конечных элементов

205

Основная идея метода конечных элементов в перемещения к состоит в том, что исследуемая конструкция заменяется ее моделью, представляющей собой объединение конечного числа простых элементов конечных размеров (рис. 7.16). Эти элементы соединяются друг с другом в конечном числе точек, называемых узлами. Вектор перемещений и в любой внутренней точке элемента выражает» ся с использованием заданных функций формы [N]   в виде u = [N] а , где

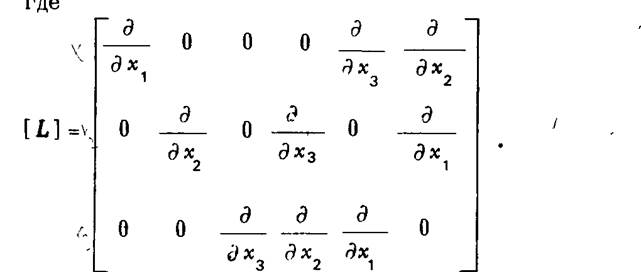
с                   се

вектор а   - набор некоторых параметров, в исходной формулировке метода совпадающих с перемещениями узлов, хотя это, вообще говоря, не обязательна

Обозначая через а совокупность искомых параметров, через которые вы­ражается приближенное решение, можно формально объединить локальные аппроксимации поля и в единую формулу

и = [ЛГ]а,                                                                                                   (7.32)

размерность вектора а в которой зависит, разумеется, от разбиения области на элементы.

В методике перемещений строятся уравнения для определения вектора а., однако метод можно приспособить и для вывода уравнений, описывающих не­установившуюся ползучесть. Здесь вместо того, чтобы строить задачу Коши на основе результатов разд. 7.3, применен (для иллюстрации) другой путь -необходимые уравнения выводятся из первого закона термодинамики.

Начнем, как это обычно делается в большинстве вариантов метода конеч­ных элементов, с формулы Грина (уравнения принципа возможных перемеще­ний). Пусть в — поле напряжений, уравновешивающее заданные массовые си­лы плотностью Ь и поверхностные нагрузки р на части граничной поверхности S   а деформации и перемещения кинематически допустимы. При этом имеет место равенство

Г

- Г iJbdV - Г_с u^TpdS= О, v